曲げ剛性と断面2次モーメント
さて、ここからが本題です。テーマは「曲げ剛性が断面2次モーメントに依存するのはなぜなのか」。
一端が固定された棒状の部材があります。下図左にあるように、その部材軸方向に x 軸をとり、さらに部材の切断面の図心を原点とする鉛直方向の y 軸、および水平方向の z 軸を考えます。
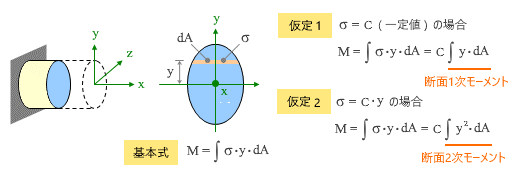
ここに何らかの外力が作用すると、切断面にそれに応じた力が発生しますが、中央の図に示すように、 z 軸から距離 y だけ離れた部分に生じている軸方向の ( 単位面積当たりの ) 応力度を σ、断面積を dA とすれば、この部分に生じている力は σ・dA。
さらに、この力による図心 z 軸回りの曲げモーメントはこれに距離 y を掛けたものになり、これを全断面について積分したものが全曲げモーメント M になる。これをあらわしたのが図の中央下部の 基本式 です。
ここで、「もし σ が断面内のどこでも一定値 C をとるとしたら」という仮定を立ててみます。図の右上の 仮定-1 ですが、この場合、先の基本式はここにあるような形に変換できます。
この C は定数なので積分記号の外に出せますが、よく見てみると、積分記号以下は「断面1次モーメント」の定義そのものになっています。
すでに説明した通り、図心軸回りの断面1次モーメントは 0 になるので、この式が成り立つのであれば M は 0 になる。つまり σ が一定値をとるのであれば、そこに曲げモーメントは存在しないことになる。
言い方を変えると、「曲げモーメントが生じているのであれば σ は一定値ではない」はずなのです。
そこで次に、「もし σ が y の1次式 C・y であらわされるとしたら」という仮定を立ててみます。これが図の右下の 仮定-2 ですが、この場合の基本式の変換形はここにある通りです。
そして、ここにある積分記号以下は「断面2次モーメント」の定義そのものになっている。
ここから、σ が y の1次式であらわされるのであれば断面2次モーメントと曲げモーメントの間には密接な関係があることが分かります。断面2次モーメントと曲げモーメントの関係は σ と y の関係の中に隠されているのです。
ところで、部材内に生じる力と変形の間には比例関係が成立します。これが有名な「フックの法則」ですが、念のために下に掲げておきます。
σ = ε ・ E
σ は応力度 注 )・ε は「ひずみ」 ( = 部材の変形量 / 元の長さ )・E はヤング係数 ( 弾性係数 ) です。
注 )
これは「単位面積当たりの力」ですが、「応力度」というのは建築工学の分野で独特に使われている用語で、一般的な材料力学ではこれを「応力」と呼びます。ただし、このテクストでは「応力度」の方を使うことにします。
さらにもう一つ、曲げ変形を考える上での重要な手掛かりがあるのですが、それは
曲げ変形している部材の変形曲線は円の一部 ( 円弧 ) をなしている
ということです ( 少々補足すると、これは「部材が厳密な円弧をなすわけではないが、その微小部分を取り出せば大局的にはそのように考えられる = 考えてよい」という意味です ) 。
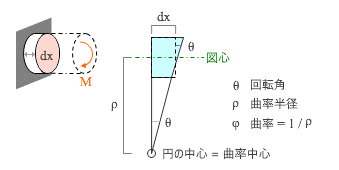
下の図を見てください。
図の右側は、左側にあるような一端が固定された部材が曲げモーメントを受けた場合の、固定端から dx の範囲にある小さな断片の変形の様子を拡大したものです。 注 )
注 )
固定端から dx の範囲ではなく、任意の位置にある長さ dx の断片を取り出す方が説明としては一般的ですが、ここでは図上での説明を分かりやすくするために「固定端から dx の範囲」にしました。
また、「円弧状に変形する」と言ったわりには直線で描かれていますが、これは dx が微小な値であればほとんど直線と考えて差し支えないし、また実際にそのように考えられているからです。
さらに付け加えると、ここにある「円の中心」は実際にはもっと遠くにあるのですが、スペースの関係があり、ここでは全体を極端にデフォルメして描いています。
この断片の左辺は固定端なので垂直のままですが、右辺は曲げの作用によって θ だけ傾くことになる。これが 回転角 です。このような傾きが生じるのは、曲げによって上辺が伸び、下辺が縮んだためです。
ところで、さきほど述べたように、この変形曲線は「円の一部」なのですから、左辺と右辺をそのまま延長していくとどこかで交わるはず。そこが円の中心 = 曲率中心 です。この円の半径を 曲率半径 と呼び、一般に ρ ( ロー ) というギリシャ文字が使われます。
さらに曲率半径の逆数、つまり 1 / ρ が 曲率 で、こちらには φ ( ファイ ) の記号が使われます。
これら ( 回転角・曲率半径・曲率 ) は構造力学の基本用語ですが、実務設計に直接登場するものではなく、つい忘れてしまいがちです。以下に、にこれらの性質を簡単にまとめておきましょう。
曲げが大きく、変形がきつい → 回転角が大きい ・ 曲率半径が小さい ・ 曲率が大きい
曲げが小さく、変形がゆるい → 回転角が小さい ・ 曲率半径が大きい ・ 曲率が小さい
本題に戻ります。
下図にあるように、長さ dx の断片の図心から y の位置にある部分のひずみ量を ⊿dx とすると、三角形の相似の関係から 式-1 注 ) が得られます。これを変形したものが 式-2 です。
この式の左辺 ⊿dx / dx は「ひずみ」に相当します。そこで、これをフックの法則の基本式に代入すると 式-3 が得られる。まさにこれこそが、私たちが求めていた「 σ と y の関係」なのでした。
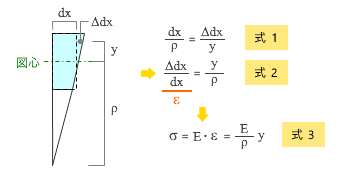
注 )
式-1 の右辺の ⊿dx は、さきほどの回転角 θ という値を使うと y ・ tanθ になりますが、θ が微小な範囲では θ = tanθ と見なせるので
⊿dx = y ・ θ
です。この関係を右辺に代入すると y が消え、この式は dx / ρ = θ です。ここで dx を 1 にすると左辺の値は曲率 φ そのものになる。つまり 曲率とは単位長さあたりの回転角 なのです。
下の 式-4 は曲げモーメントと応力度の関係をあらわす基本式の再掲です。
曲げモーメントと曲げ応力度の関係を表わす基本式を下に再掲しました ( 式-4 )。
ここにある σ を 式-3 の値で置き換えると 式-5 が得られますが、先に述べたように、ここにある積分記号以下は断面2次モーメントの定義そのものです。そこで、これを記号 I で置き換えて整理すると 式-6 が得られる。
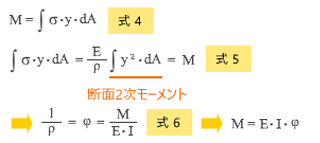
この式は私たちに
断面2次モーメント I が大きいほど曲率半径 ρ が大きくなり曲率 φ が小さくなる。
つまり、曲げ剛性が大きくなって変形が小さくなる。
ことを教えています。
これが最終結論になりますが、ついでに、この σ がどのような値をとるかについても考えておきましょう。
式-3 を変形すると下の 式-7 が得られます。これは 式-6 にある 1 / ρ という値の別の表現なので、両者の右辺を等置して整理したものが 式-8 です。ここから、「図心からの距離 y が大きいほど曲げ応力度 σ が大きくなる」ことが分かります。
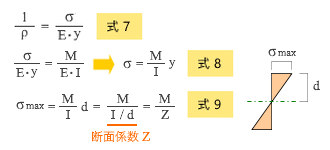
したがって、曲げ応力度は断面の外縁部で最も大きくなるはずなので、式-8 にある y を図心から断面外縁部までの距離 d で置き換えれば、それが σ の最大値 σmax をあらわすことになる。
これが 式-9 ですが、これをさらに変形したものの分母、つまり断面2次モーメント I を d で割ったものが 断面係数 と呼ばれるわけです ( これまた「何をいまさら」でしょうが ) 。
( その1 終わり )
前へ | 1 | 2 | 3 |
|