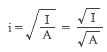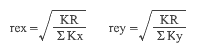断面2次モーメント
前項で紹介した断面1次モーメントの「1次」とは何なのかというと、これは面積に長さを「1回だけ」掛けているからです。面積とは長さを2回掛けたものなので、結局、断面1次モーメントは「長さの 3 乗」という次元をもつことになる。
これに対する断面2次モーメントとは面積に長さを「2回」掛けたものです。
したがって、こちらは「長さの 4 乗」という次元をもつという、ただそれだけの話ですが、この場合に何が大きく違ってくるかというと、( 長さが負であってもそれを2回掛ければ正になるので ) 断面2次モーメントの値は必ず 0 より大きくなる のです。
図心回りの断面1次モーメントは 0 になるが、断面2次モーメントの方は 0 にはなりません。
この「図心回りの断面2次モーメント」とは、その断面がどこにあるかに関係なく潜在的に保持しているポテンシャル値と考えられますから、回転軸から L の距離にある面積 A の物体の断面2次モーメントは下の式であらわされることになります。
断面2次モーメント = 図心軸回りの断面2次モーメント + A × L2
図心軸回りの断面2次モーメント ( Iox および Ioy ) の一般的な表現を下図左に、任意の回転軸に対する断面2次モーメント ( Ix および Iy ) の考え方を下図右に示しました。
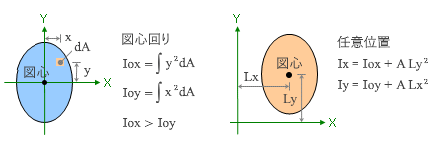
左側の図 ( 図心軸回りの断面2次モーメント ) をもう一度見てください。
ここで、「 Iox の方が Ioy よりも大きくなる」ことは簡単に察しがつくでしょう。なぜなら、回転軸から遠い部分に断面積をもつものほど断面2次モーメントが大きくなるからです。
本当にそうなのかどうかは座標軸を少しずつ回転 ( 図形の方を回転させても同じ ) させながら断面2次モーメントを逐一計算してみればいいのですが、しかしそんな手間をかけるまでもなく、以下のようなことが分かっています。
どこかに対称軸をもつ断面では、その軸に関する断面2次モーメントが極大値または極小値を与え、それと直交する軸に関する断面2次モーメントが極小値または極大値を与える
これが 主軸 と呼ばれるもので、最大値を与える方を 強軸、もう一方を 弱軸 と呼ぶ――このあたりも「何をいまさら」と言われそうなので、ここでは長方形やH形ではなく、もう少し複雑な山形鋼 ( アングル ) の断面を取り上げてみましょう。
下図にあるように、この断面の対称軸は斜め 45 度方向の u 軸にあります。これが主軸の一つですから、もう一つの主軸は図心を原点としてこれに直交する v 軸になるはず。ではこの時、どちらの軸回りが「強軸」になるか?
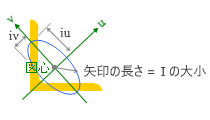
形鋼の断面表などの凡例図に楕円形が描き込まれているのを見たことがあると思います。上の図にある青い線です。
ここにある通り、図心が楕円の中心になっていますが、この中心から任意の傾きをもつ直線を引いて楕円との交点を求めれば、中心からその交点までの距離が ( その傾きをもつ座標軸に関する ) 断面2次モーメントの大小をあらわすのです。
この場合、それが最も大きくなるのは楕円の長径に相当する iu で、最も小さくなるのは短径に相当する iv ですが、ここから u 軸回りの断面2次モーメントが極大値、v 軸回りが極小値になることが分かります。
これが 断面2次半径 と呼ばれる値で、一般に小文字の i の記号が使われます。
とはいえ、これは断面2次モーメントそのものの値ではなく、断面2次モーメントの平方根に比例した値です。その理由は、そのような操作を施すと図心回りにきれいな楕円を描くことができて好都合だからなのですが、このあたりの理論は略し、以下に計算式だけを掲げておきます。
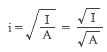
ここでは、断面2次モーメントの平方根に対する比例定数が断面積 A の平方根の逆数になっています ( 断面積 A は回転軸の向きに関係なく一定値をとる ) 。したがって、これは「長さ」の次元を持つことになる。さらにこの式を変形すると
I = i 2 × A
ですが、見ての通り、これは断面2次モーメントの定義そのものです。
つまり、i を既知とした時の断面2次モーメントは、「図心から i だけ離れた位置に全断面積 A が集中して存在する」という仮定のもとに得ることができるのです。
前項で説明した通り、偏心率の検討に使用する「重心位置」「剛心位置」は「断面1次モーメント」の考え方に基づいたものですが、偏心率の値そのものの計算には「断面2次モーメント」あるいは「断面2次半径」という値が使われています。
まずは「剛心回りのねじり剛性 KR 」ですが、これは下のように定義されている。
KR = Σ ( Kx・y 2 ) + Σ ( Ky・x 2 )
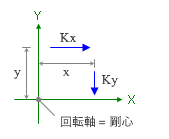
ここにある Kx および Ky はそれぞれ XY 方向に関する耐震要素の水平剛性ですが、これは「断面積」に置き換えることができます。また、x および y は剛心から各耐震要素までの距離ですが、「剛心」とは「剛性の重心 = 断面の図心」にほかなりません。
ようするに、上にあるのは「断面2次モーメント」を表わす式で、「剛心回りのねじり剛性」とは「図心回りの断面2次モーメント」のことなのです ( ただし下図にある通り、ここで考えているのは、この画面に直交する方向に回転軸があり、画面に平行な方向に X または Y 方向の力が作用しているものとしたものなので、それぞれの力による曲げモーメントを加算している ) 。
ということになれば、ここには当然、剛心を中心とした「断面2次半径」の楕円を描くことができます。それが偏心率の規定にある「弾力半径 re 」の値で、X および Y 方向に関して以下のように定義されています。
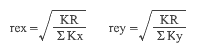
この KR は I に、ΣKx と ΣKy は ΣA に置き換えることができます。
ねじり剛性 ( = 断面2次モーメント ) が大きいほど、あるいは弾力半径 ( = 断面2次半径 ) が大きいほど回転剛性が大きい ( = 変形しにくい ) のです。
前へ | 1 | 2 | 3 | 次へ
|