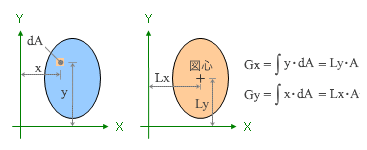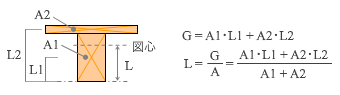|
何をいまさら構造力学・その 1 ― 断面2次モーメントと曲げ剛性 ―
構造力学関係の入門書であれば、まず例外なく、「断面2次モーメントと曲げ剛性の間には密接な関係がある」というようなことが書かれていて、代表的な断面に関する断面2次モーメントの算定式が載っていたりします。
そして、梁幅を2倍にしても曲げ剛性は2倍になるだけだが、梁せいを2倍にすると曲げ剛性は8倍になる ( だから曲げ剛性はほとんど「梁せい」によって決定される ) というような説明がなされるわけですが、その一方、「断面2次モーメントが大きくなると なぜ 曲げ剛性が大きくなるのか」まで説いたものは少ない気がします。
そこで、最初にそのあたりを考えたいのですが、その前に、基本的な事項について少々おさらいしておきましょう。
断面1次モーメント
ある力が作用している時、それが任意の回転軸の回りに及ぼす曲げモーメントの値は、その力の大きさに力の作用位置と回転軸の間の距離を掛けたものになる。複数の力が作用しているのであれば、その個々の力による曲げモーメントを足し合わせればよい――このあたりは「何をいまさら」でしょうが、下図左にあらわしました。
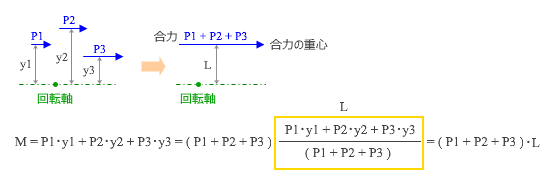
ところで、ここにある P1・P2・P3 という ( 同じ向きに作用する ) 3つの力は P1 + P2 + P3 という1つの力に置き換えることができます。これが 合力 ですが、私たちは「回転軸回りに作用する全曲げモーメント M 」の値を知っているので、ここから合力の作用位置 L を簡単に求めることができる。その計算式は図に示した通りです。この合力の作用位置が3つの力の 重心 と呼ばれるわけです。
ここで、上図の回転軸を少しずつ上の方にずらすことを考えてみます。
すると距離 L は小さくなりますから、それにつれて曲げモーメント M も小さくなる。そして L が 0 の時 M も 0 になりますが、この値が 0 ということは
P1・y1+ P2・y2+ P3・y3 = 0
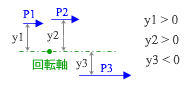
です。ここで力 P1・P2・P3 はすべて正の向きに作用しているので、この等式が成り立つには距離 y1・y2・y3 の正負符号が違っていなければなりません。
慣習にしたがい、回転軸よりも上の方向を正、下の方向を負の符号であらわすと、回転軸よりも上にある力は時計回りの曲げ、下の力は反時計回りの曲げをもたらすので、下図にある通り、それらが打ち消しあって曲げモーメントが 0 になる。
次に、ある部材の軸方向に力 P が作用している状態を考えてみます。下図の一番左側です。
この時の回転軸は材軸と直交する方向に存在しますが、この切断面を正面から見た状態が中央の図です ( 左の図とは視点が 90 度回転しているので、力は画面と直交する方向に作用していることになる ) 。
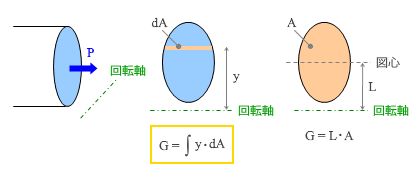
この力が断面内に均等に分布しているものとすると、「回転軸から一定の距離にある力の大きさ」は「回転軸から一定の距離にある断面積」に等しい。もう少し具体的にいえば、「断面内に均等に一定の応力度が生じているので、面積の値がそのまま力の大きさになる」わけですが、これが図中の dAです。
したがって、この部分の回転軸からの距離を y とすると、これによって生じる曲げモーメントは y・dA で、全体の曲げモーメントはこれを全断面について積分したものになる。この値が 断面1次モーメント で、ここでは G の記号であらわしています ( 簡略化しているが、ここにある積分記号は「全断面についての積分」の意味 ) 。
これはまさしく、さきほどの説明にあった「複数の力が回転軸の回りにもたらす曲げモーメント」と同じもので、この値は「それらの力の合計に重心位置までの距離を掛けたもの」に等しくなる。
ここにいう「それらの力の合計」は、ここでは図形の「全断面積」に相当しますから、結局、
断面1次モーメント = 回転軸から図形の重心位置までの距離 ( L ) × 図形の全断面積 ( A )
ということになります。これが図の一番右側です。断面内に一様に力が分布しているものの重心位置はその断面の幾何学的な形状から決定されるで、特に 図心と呼ばれます。
ここで注意しておきたいのは、上式の L は負の値をとることがある、ということです。
この場合、断面1次モーメントの値も負になりますが、先に説明した通り、これは回転軸と図心 ( 重心 ) 位置の上下関係によって決まります。そして、回転軸が図心位置にある場合は断面1次モーメントが 0 になる。
つまり 図心回りの断面1次モーメントは 0 になる のです。
こでは水平軸 ( X 軸 ) 回りの回転だけを考えましたが、同様に垂直軸 ( Y 軸 ) 回りの回転も存在します。これらの軸を考えた時の X 軸回りの断面1次モーメント Gx と Y 軸回りの断面1次モーメント Gy の一般的な表現を下図に示しておきます。
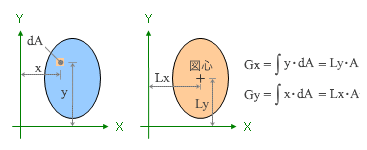
ただし、この値が構造計算書に表立って登場することはほとんどありません。予備計算的に使われることがあるとしたら、たとえば「スラブ付き梁の図心位置を求める」というようなケースでしょうか。
下図に示すように、梁とスラブの個々の断面一次モーメントが既知であれば、これらの和が合成断面の一次モーメントになり、これを全断面積で割ったものが合成断面の図心 ( 重心 ) になるのです。
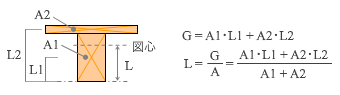
それからもう一つ、この考え方の応用ということであれば、偏心率の検討に使用される「重心位置」や「剛心位置」の計算があります。その計算式は略しますが、ここまで述べてきた「断面積」を「柱軸力」あるいは「水平剛性」に置き換えて「重心」を求めたものであることは容易に理解できるでしょう。
| 1 | 2 | 3 | 次へ
|