|
何をいまさら構造力学・その 3 ― 剪断力と剪断変形 ―
日本建築学会の計算規準によれば、鉄筋コンクリート部材の ( 補強筋の効果を除いた ) 剪断耐力 Qa は以下の式で計算してよいことになっています。
Qa = b × j × fs ( 記号の意味については省略 )
ところで、ここになぜ ( 曲げ耐力を求めるための ) 「応力中心間距離 j 」という値が登場しているのでしょうか?
剪断応力度とは剪断力を断面積で割ったものなのだから、本来ならば、この部分は「梁せい」になるはずではないか? ( 実際、耐震壁の剪断耐力を求める時には「壁のせい」 が使われている ) ――私はそのような疑問をもっていました。
そして、その正確な理由を知ったのは、設計の仕事に従事するようになってかなり長い年月を経過した後だったように記憶しています。
そういうわけで、今回の主要なテーマは「剪断力と剪断変形」ですが、上のようなこともあるので、最後の方で「耐力」についても若干ふれることにしました。
平面応力と主応力
剪断変形とは長方形のものが平行四辺形になる ( = ずれる ) 状態をあらわし、そのような変形をもたらす力が剪断力である、というようなことをあらためて説明する必要はないでしょう。
建物を構成する部材が「 ( 曲げ変形を伴わない ) 剪断変形だけが生じている」という状態になることはほとんどありませんが、しかし低層の耐震壁については「曲げ変形の影響は微小なので、それを無視して剪断変形だけを考えてもよい」とされています。したがって、これが剪断変形を考える上での格好の教材になるでしょう。
下図にあるのは、下辺が固定されているスパン長 L・階高 H の耐震壁に水平力 P が作用した状態です。
この時、耐震壁の枠組みの上下辺に水平方向の力 Qh ( = P ) が発生しますが、これによって発生する曲げモーメント ( = P・H ) に対する釣り合い上、左右辺にも鉛直方向の力 Qv ( = P・H / L ) が発生します。
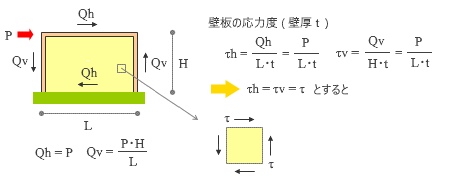
この応力を単位長さの当たりのものに換算し、さらに壁厚で割ったものが壁板の応力度ということになりますが、ここにある通り、水平方向ならびに鉛直方向に関してこれらは同じ値をとります。 注 )
そこでこれに τ ( タウ ) という記号を割り当て、壁板から単位長さをもつ微小な正方形を取り出してみると、その応力状態は上図右下のようなものになっていると考えられます。
注 )
ここで水平方向と鉛直方向の応力度が同じ値になるのは偶然ではありません。もし鉛直方向の τ が水平方向と異なる値をとっていたら、この要素は「回転」してしまう。ようするに、鉛直方向に生じている τ は水平方向の τ によって生じる回転変形を抑え込む役目を担っていることになるのです。この状態が「剪断変形」です。
上に掲げたような状態を 平面応力 と呼んでいます。これは平面板がその「面内」に荷重を受けて「面内」で変形する状態、別の言い方をすると、面に直交する方向の荷重や変形は存在しない ( 考えないことにする ) 状態です。
さきほどは壁板から正方形の要素を切り出しましたが、形状は三角形でも五角形でも構いません。下図に示すように、平面板の応力状態は、境界線に沿って生じている 剪断応力度――記号 τ が使用される――と、境界線に直交する方向に生じている 垂直応力度――記号 σ が使用される――という二つの値によってあらわされるのです。
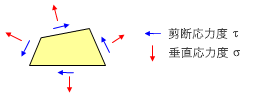
そしてもう一つ、ここには以下のような重要な性質があります。
平面板の応力状態は、それがいずれかの方向に「引っ張られた状態」と「押し込まれた状態」に置き換えることができる。そしてこの時、「引っ張られる方向」と「押し込まれる方向」は必ず直交する。
この時の引張り ( あるいは圧縮 ) 応力が 主応力、その力の向きが 主応力方向 です。
さきほどの図 ( 耐震壁から切り出した正方形要素の応力 ) を下に再掲しますが、この状態は「剪断応力度 τ のみがあり、垂直応力度 σ が 0 になっている」状態です。
さきほど「低層の耐震壁では剪断変形のみを考え曲げ変形を無視してもよい」と述べましたが、これは「 σ の値は小さいのでこれを 0 と見なす」という意味なのでした。この状態は純剪断と呼ばれます。
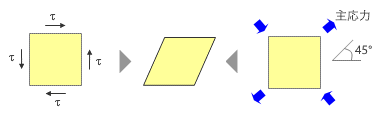
で、ご存知の通り、この正方形は剪断変形して平行四辺形に変わります。これが図の中央ですが、よく見てみると、これは正方形をその対角線方向、つまり 45 度方向に引っ張った――あるいは -45 度方向に押し込んだ――形になっている。図の右側に示したように、ここでは 45 度方向に「主応力」が存在するのです。 注 )
注 )
大きな地震力を受けた耐震壁に「剪断ひび割れ」が入った状態を写真か何かで見かけたことがあるかもしれませんが、この時のひび割れは必ず「斜め」に入ります。これは、主応力によって壁板が斜め方向に引っ張られたことをあらわすものです。
この時の主応力によって具体的にどのような応力度が生じるのかについては、たとえば下図のように、正方形を左上がりの対角線で二分し、45 度方向の座標軸 u 及び v を設定して各々の軸に関する力の釣り合いを考えれば分かります。ここで、斜辺 AC 上に存在する垂直応力度 σo に斜辺の長さを掛けたものが τ の v 軸方向成分に等しいことから、下図にあるような結果が得られることが分かります。
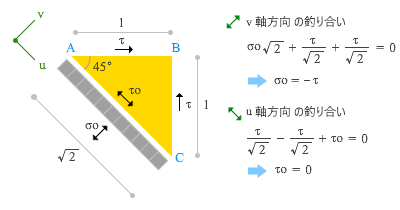
この時もう一つ注意しておきたいのは、τ の u 軸方向の成分が互いに打ち消し合って 0 になることです。したがって、斜辺 AC の剪断応力度 τo は 0 でなければならないことになる。ここから
主応力は、その方向に関する剪断応力度が 0 になるような向きに発生する
という結論が導かれます。
これをもう少し具体的にイメージしたいのであれば、さきほどの壁板の中から 45 度方向に傾斜した正方形要素を切り出した状態を考えてみてください。下図にあるように、この要素の各辺には垂直応力度 σ だけが存在し、剪断応力度 τ は 0 になるのです。
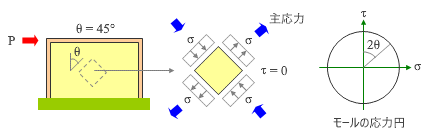
ここまでの話を整理します。
上の図にあるように、壁板から切り出した矩形断面の鉛直軸に対する傾きを θ とすると、これが 0 の場合は τ が最大値をとり σ が 0 になる。一方、θ が 45 度 ( 主応力方向 ) の場合は σ が最大値をとって τ が 0 になる。
ということは、θ がそれ以外の値をとる場合には「何がしかの σ 」と「何がしかの τ 」が生じるわけですが、実はここには「 σ の2乗と τ の2乗の和は一定になる」という性質があります。 注 )
注 )
このような関係が成り立つのは、ここで取り扱っているような「純剪断」の場合に限られます。そうでない場合も、以下に述べる「モールの応力円」という考え方は成り立つのですが、ただし、円の中心が原点ではなくなります。
その証明は略して簡単な紹介だけにしますが、つまりこの結果、直交座標軸上に σ と τ をとると、その関係は一つの円によって表わされることになる。これが上の図の右に示したグラフですが、ただしここでは、実際の θ を 2 倍にした値を使用します。ここから、θ が 0 の場合に τ が最大値をとって σ が 0 になり、θ が 45 度 ( グラフ上では 90 度 ) の場合は σ が最大値をとって τ が 0 になることが確認できるでしょう。
これが モールの応力円 と呼ばれるものですすが、( もし忘れてしまったのなら ) 名前だけでも思い出しておきましょう。
| 1 | 2 | 3 | 4 | 次へ
|