|
何をいまさら構造力学・その 2 ― 曲げモーメントと曲げ変形 ―
日常の構造計算で使われる数値の基本単位は「力」か「長さ」――これを2乗した「面積」とか4乗した「断面2次モーメント」などを含む――にほぼ限られます。この「力」に「長さ」を掛けたものが「曲げモーメント」と呼ばれる別種の力で、これが構造物の断面を決定する最も重要なファクターになるのはご存知の通りです。
ところで、この「曲げモーメント」は部材に「回転」という変形をもたらし、その大きさは「角度」という単位――構造力学では360度を 2π としたラジアン ( rad ) という無次元量が使用される――であらわされるのですが、そのような値が構造計算で直接使われることはほとんどありません。
しかし、構造力学が「力と変形の関係」を追求するものだとしたら、「曲げモーメントと回転変形の関係」は最も基礎的な概念になっているはずです。それが日常の構造計算にあらわれてこないのは「関係ない」からではなく、「隠されている」からに過ぎません。
というわけで、このあたりをちゃんとおさえておくことにしましょう。
曲げモーメントと回転角
「その 1 」で大切なことを言い忘れてました。
下図は、片持ち梁の側面に鉛直の線を描き入れ、それが曲げ変形した後にどのように見えるかを図示したものですが、この時、「平面を形成していた任意位置の切断面は変形後も平面を保持する」と考える。つまり、下図にある梁の側面に描き入れた赤い線は部材の変形後でも直線を保つと考えるのですが、これは力と変形の関係を考える上での大前提で、平面保持の仮定 と呼ばれています。
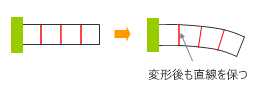
そしてもう一つの前提は 部材の変形曲線は円弧をなす というものでした。
その円の半径は曲げモーメントの大きさ M と部材の断面2次モーメント I ならびにヤング係数 E によって決定される。ということは、もし上図にある片持ち梁の全長にわたって同じ大きさの曲げモーメントが作用しているのであれば、この変形曲線の全体が一つの円の円周上にあることになり、図の右にある3本の赤い線は一点で交わるはず。
このあたりを下図にあらわしましたが、ここにある曲率半径 ρ・曲率 φ の関係式は「その 1」の復習です。
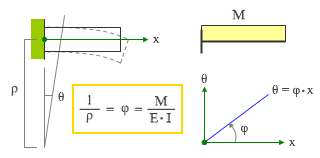
ここで材軸に沿った方向に x 軸を考えてみると、曲率半径 ρ は一定なので、回転角 θ は x の値に比例して大きくなります。この時の x と θ の関係が右下のグラフですが、この直線の傾きが曲率 φ です ( 曲率とは単位長さ当たりの回転角である、という話を思い出してください ) 。
これだけのことならばいたって簡単ですが、しかしこれは「曲げモーメントが全長にわたって一定である」と仮定した場合の話です。
そもそも、片持ち梁の曲げモーメントが全長にわたって一定であるという仮定自体があまり現実的とは言えないでしょう。たとえば、先端に力が作用した時の曲げモーメントは直線的に分布し、先端で 0・固定端で最大値をとる ( 下図左 ) 。ではこの時、回転角 θ はどのように分布するか?
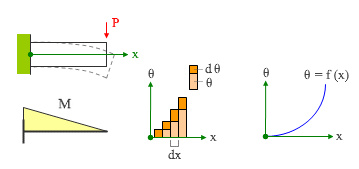
まず、以下のようなことが言えそうです。
-
回転角 θ は固定端 ( x = 0 ) で 0 になり、そこから遠ざかるにつれて大きくなり先端で最大値をとるはず。なぜならば、任意位置の回転角 θ とは、そこより左側にある回転角の累積値になると考えられるから。
-
しかしこの時、θ の値が直線的に増加するわけではない。なぜならば、各位置における曲率半径が違ってくる――つまりさきほどと異なり、変形曲線が同一の円周上にあるわけではないから。
上図の中央にあるのは、上記 A の考え方をさらに具体的にしたものです。
ここには、部材を dx の長さをもつ複数の要素に分割した上での各要素の回転角をあらわしましたが、ここから、ある位置における回転角とは、左側の要素の回転角 θ に、その要素内で生じる回転角 dθ を加えたものである、ということが分かります。そして θ は x = 0 の位置で 0 になるのですから、
-
ある位置における θ を得るには、それよりも左側にある部分を微小な区間 dx に分割し、それらの区間における dθ を積分すればよい
ということが分かる。さらに、
-
全体としての曲げモーメントは一定ではないが、区間 dx が微小であれば、その区間内の曲げモーメントは一定であると考えてもよいのではないか。
-
であるのならば、その区間内では、私たちが知っている曲率と回転角の関係が成り立つはずである。
ということも言えそうです。
下図は、上記 3 にある「微小区間 dx においても曲率と回転角の関係が成立する」ことを証明し、さらに上記 1 の考え方にしたがって、原点から uu の位置における回転角 θu の計算式を導いたものです。
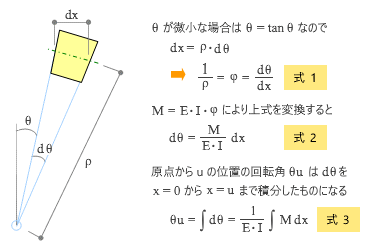
上の 式-3 にある曲げモーメント M は x の1次式になり、片持ち梁の全長を L とすれば M = P・( L - x ) になる。これを代入して積分すれば θ と x の関係になるわけです。
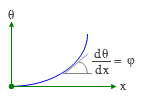
ここでは詳細は略して結論だけをいうと、この θ は x の2次式になり、下のようなグラフが描けます。任意の位置でこの曲線に引いた接線の勾配が dθ / dx、つまりその位置における曲率 φ になることはすでにお分かりでしょう。
| 1 | 2 | 次へ
| 



