|
平板の曲げ ここでは「かんたん平面板」で扱っている「平板の曲げ」の考え方を紹介します。これは鉛直方向に外力を受ける板のたわみと曲げモーメントを求めるものです。平面をあらわす xy 軸だけでなく、それに直交する z 軸まであるのですから、これはどう見ても三次元モデルでしょう。が、ここに何らかの仮定を設けることで二次元モデルに縮小してしまおう、というのが「平板の曲げ」の考え方です。 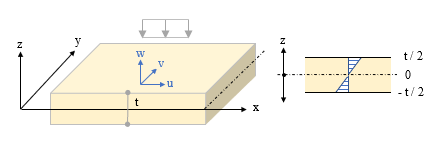 とりあえず、x・y・z 軸方向に対応した要素内の変位成分を、u・v・w としておきます ( 上図左 ) 。 そして z 軸の原点 ( z = 0 ) を板の厚さ t の中心部にとります。 さらに、図の右のように、ここが板の中立軸で、断面内の変位量はこの位置で 0 になり、- t / 2 から t / 2 の範囲の距離 z に比例して変化するものと考える。ようするに、梁理論における平面保持の仮定 ( 中立軸に直交する断面は変形後も中立軸に直交する ) です。 次の仮定は「その 4」で紹介した「平面応力」と同じです。z 方向の応力は生じないものと考えて σz = τzx ( τxz ) = τzy ( τyz ) = 0 とします。 鉛直方向に力が作用しているのならその方向にせん断力が発生するはずですが、「薄い板」を対象にしているのでせん断変形は無視できる、ということなのでしょう。 つまり、ここでは「曲げ変形」のみを考えるのです。 平面応力なので、応力 σ とひずみ ε の各成分は σ = { σx σy τxy } ε = { εx εy γxy } です。ただし、ここで問題にしているのは平面応力のような「伸び縮み」ではなく「曲げ変形」ですから、考え方は少し違ってくるでしょう。そのあたりから見ていくことにします。 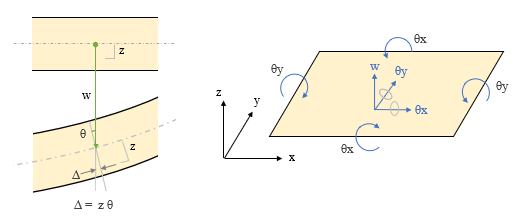 上図左は、板が外力の作用によって鉛直方向に変位 w が生じた時、断面の中立軸から z の距離にある点の変位 Δ の値を確認したものです。 ここには曲げによる回転角 θ が生じます。そして変位は z と θ の積になる。だからここでは、「変位とは回転角 θ そのものである」としても構わないように気がします。 そこで上図右のように、x 軸回りの回転角 θx と y 軸回りの回転角 θy が要素に生じている状態を考えることにします。この時の x 方向の変位 u と y 方向の変位 v は u = z・θy v = z・θx なので、u と v を θx と θy で置き換えてしまうと、ここにあるように、要素の変位成分は { θx θy w } の三つになりました。 次はこの変位成分に対応する「力」の方ですが、回転角を生じさせるのは「曲げモーメント」です。 そこで x 軸回りの曲げモーメントを mx、y 軸回りの曲げモーメントを my とすると、最終的に、節点の自由度成分は下図左、節点力成分は下図右のようになります。 この両者を関係づけるのが要素の剛性マトリクス [ Ke ] です。 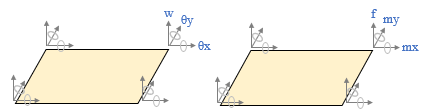 ━━なお、余計なことに頭を悩ますことがないよう、ここでは、座標軸と回転の正負方向はまったく考慮しないで書いています。そういうことが気になる方は適宜読み替えるか、または別の参考書にあたってください。 ● ひずみベクトル { ε } 平面応力のひずみ成分の式中の u に z・θy、v に z・θx を代入すると下式になります。 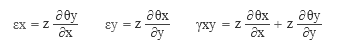 ところで、構造力学によれば、曲げを受ける材に生ずる回転角 ( たわみ角 ) とは曲げたわみ量を距離で微分したものです。つまり 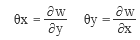 なので、これを先の式に代入すると 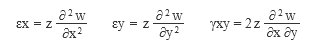 になります。これにより、ひずみ成分のすべてが変位 w から得られることになりました。 ただし、ここには z という変数が含まれています。これをなんとかする必要があるでしょう。 ● 応力ベクトル { σ } ひずみ成分の中に z という変数があるのは、ようするに、板の中から z が一定となるような z 軸と直交する平面を切り出した時、そこでは平面応力の関係 { σ } = [ D ] { ε } が成立している、という意味です。 しかし、本当に知りたいのは板の厚さ t の「全体」に関する値です。 そこで、z を - t / 2 から t / 2 の範囲で積分することにします。 下図の左は厚さ t の板の内部の σ の分布ですが、ご存知の通り、これを積分すると「曲げモーメント」という力になります。そこで、応力成分 σx σy τxy に対応する曲げモーメントを Mx My Mxy としてあらわした積分式が下図の右です。 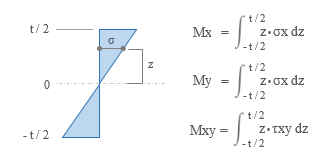 この式中にある σx σy τxy にそれぞれ平面応力の関係 { σ } = [ D ] { ε } を代入して積分するわけですが、途中を省略して結論だけを書くと、以下のような関係が得られます。 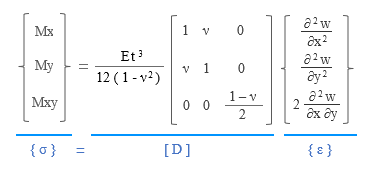 ここで、左辺の { Mx My Mxy } を応力ベクトル { u } に、右辺を [ D ] と { ε } に読み替えてしまえば、これを平面応力として解くことができるはず、というのが「平板の曲げ」の仕組みなのでした。 ところで、ここにある Mxy とは「せん断力による曲げモーメント」です。耳慣れない言葉なので、下に図示しました。 ここに見えている辺に対向する側ではせん断力の向きが逆なので、逆向きの曲げモーメントが生じていることになる。ようするに、Mxy とは「ねじりモーメント」のことなのでした。 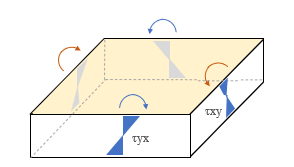 その後の手順は平面応力と基本的に変わらないので省略します。なお、ここでは形状関数の成分が位置の一次関数にはならないので、「その 5」にあるような積分点を使うことになります。 主応力 これは有限要素法の問題というより、その結果の評価に関わる問題ですが、最後に「主応力」という話題を取り上げておきます。下図左は二次元平面の微小要素の応力を再掲したものですが、ここにある応力の方向は全体座標軸の方向に一致します。つまり全体座標軸の取り方を変えればそれに伴って応力の値も変わってしまうわけですが、全体座標軸の取り方に依存しない応力を知りたい場合もあるでしょう。 そこで、図の右にあるようにこれを回転させてみると、それにつれて応力成分 σx σy τxy の値が変化します。どう変化するかはモールの応力円 ( σ と τ の関係を円周上にあらわしたもの ) などで確認できますが、いずれにせよ、どこかに「 τ が 0 で応力が σ だけになる」ような状態が存在する。 その時の σ の大きい方の値が第 1 主応力 σ1、小さい方が第 2 主応力 σ2 で、これらの方向は 90 度ずれることになります。各応力成分から σ1 と σ2、およびその角度 θ を求めるのは比較的簡単ですが、具体的な式は省きます。 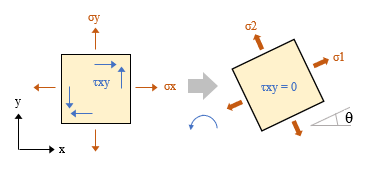 主応力の分かりやすい例として、下図のような、σ が 0 で τ だけが存在しているようなものを考えてみます。 元の正方形は変形して平行四辺形になりますが、図の右にあるように、これを 45 度傾けてみると、一方向に引張力、もう一方の側に圧縮力を受けたのと同じ変形状態になっていることが分かります。この時の引張力または圧縮力が主応力です。 地震で大きな横力を受けた壁に 45 度方向の亀裂が入っている写真をどこかで見たことがあるかもしれません。これは、その亀裂に直交する方向に引張力が作用したことをあらわすものです。 この例からも分かるように、主応力による評価は、脆性的な破壊をするものの検証時に多く用いられます。 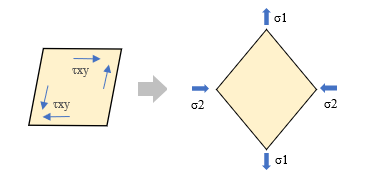 ところで、力学上では引張力に正符号・圧縮力に負符号を付ける習慣があります ( 国によっては逆にする所もあるらしいですが ) 。その結果、一般に σ1 は引張力で σ2 は圧縮力になる。 ここから、「第 1 主応力はその方向に材が引っ張られていることをあらわす」とよく言われます。たいていの場合はそれで正しいのですが、しかし先に書いたように、本来、σ1 と σ2 は値の「大小」をあらわしたものに過ぎません。ですから、σ1 が圧縮力になることだってあるのです。このことは頭に入れておいた方がいいと思います。 ( 終わり ) その1 その2 その3 その4 その5 その6 |