|
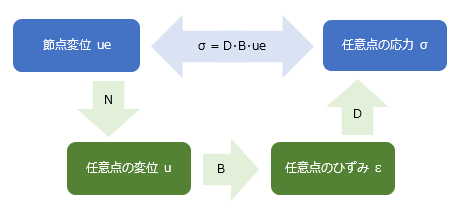
有限要素法の基本式 節点の外力ベクトル { f } は構造物の全体剛性マトリクス [ K ] と節点の変位ベクトル { u } の積として{ f } = [ K ] { u } のようにあらわされる。これが 外力 - 節点変位の関係。 ここで外力ベクトルは既知なので、全体剛性マトリクスを作ることができれば、その逆マトリクスと外力ベクトルの積により { u } = [ K ] -1 { f } で変位ベクトル、すなわち各節点の変位量を求めることができる。 ━━というのが有限要素法の基本的な流れですが、これはおなじみの変位法 ( 繰り返しますが、ここでは便宜的に、線材を対象とした有限要素法をこの名前で呼んでいます ) と同じです。 そこでまず、復習をかねながら、線材を対象とした変位法の解析を追ってみることにします。 トラス材の例題 下図のような二次元の全体座標系上で 3 節点 2 部材のトラス構造を例題として取り上げます ( 拘束条件が何もないので実際には不安定構造ですが、あくまでも説明用 ) 。トラス材なので節点の回転 ( = 部材の曲げ ) は考えませんから、各節点には全体座標系の x および y 方向という 2 つの自由度 ( 未知の変位成分 ) しかありません。これらの各成分を順に ( u1x, u1y ) ... とすると、これが計 6 個の成分をもつ変位ベクトル { u } です。 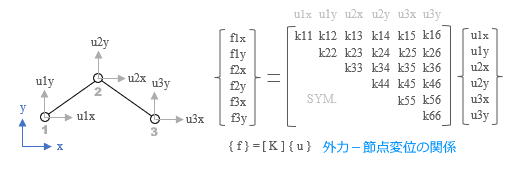 これに対し、各自由度に対応する外力成分を同様に ( f1x, f1y ) ... としたものが外力ベクトル { f } で、これらを全体剛性マトリクス [ K ] を介して結びつけたのが 外力 - 節点変位の関係 です ( 上図右 ) 。 ここで、全体剛性マトリクスの成分 kij は「自由度 j に単位の変形を与えるために自由度 i に加えるべき力」をあらわします。ここには一般に kij = kji という関係が成立する ( 相反定理 ) ので、このマトリクスは「対称マトリクス」です。したがって、上ではマトリクスの右上半分だけを書いています。 この全体剛性マトリクスは「要素の剛性マトリクス」を要素数分重ね合わせて作ります。そして要素の剛性マトリクスは「応力 - ひずみ」の関係から導かれるのですが、以下、そのあたりを見ていきます。 応力 - ひずみの関係 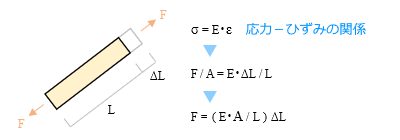 上図にあるような長さ L の要素が大きさ F の外力を受けると要素内に応力 σ ( シグマ ) が発生します。要素の断面積を A とすれば、この値は F / A 。 この力によって要素の長さが伸縮しますが、その伸縮量 ΔLが 変形です。 これに対し、元の長さに対する変形の度合いをあらわす無次元量が ひずみ で、一般に ε ( エプシロン ) の記号が使われます。この場合は ΔL / L 。 そして応力 σ とひずみ ε の間にはヤング係数 E を介して σ = E・ε の関係がある。これが 応力 - ひずみの関係 です。 上図の右にあるように、この式をさらに書き直すと以下の関係が得られます。 F = ( E A / L ) ΔL ここで ΔL を 1 とした時の右辺の値 E A / L が 剛性、すなわち「単位の変形を与えるために材に加える力」です。 ところで、ここにある変形量 ΔL とは「材が軸方向に沿ってそのまま変形した時の伸縮量」をあらわしたものです。しかしもちろん、いつもそういう風に変形するわけではありませんから、次に、これを両端の節点の変位量からあらわすことを考えます。 下図は、長さ L の材の両端に u1 および u2 という節点変位 ( ベクトル量 ) が生じ、結果的に長さが L’ になった状態です。分かりやすくするために原点 O からのベクトルを描いておきました。 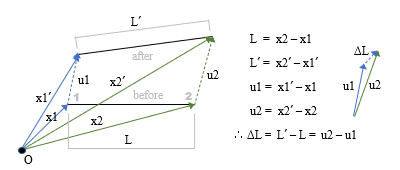 図の右にあるベクトル演算を見ていただきたいのですが、ここから ΔL = u2 – u1 なので、これを使ってさきほどの式を書き換えると F = ( E・A / L ) ( u2 – u1 ) になります。これが「力と節点変位の関係」です ( なお、材の両端では力の向きが違うので正負符号が反転しますが、そのあたりは気にせず先に進むことにします ) 。 要素の剛性マトリクス 以上を踏まえて要素の剛性マトリクスを作りますが、この剛性マトリクスは最終的に全体剛性マトリクスに組み込まれるものなので、自由度の向きを全体座標系に合わせる必要があるでしょう。ここまでの話は材軸方向の力と変位の関係をあらわしたものでしたから、それを適切に変換しなければなりません。そのあたりを、先の例題にある右上がりの要素 ( 1 - 2 ) について見ていきます。 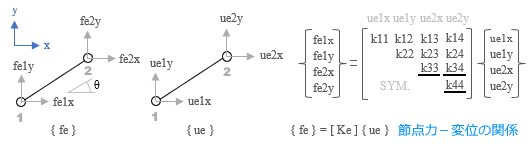 上図左のように、材の両端に全体の自由度方向と一致する力の成分 fe1x, fe1y, fe2x, fe2y を考え、これをベクトル { fe } とする。さらにその右のように、変位についても成分 ue1x, ue1y, ue2x, ue2y を考え、これをベクトル { ue } とします。 その上で、さきほどの諸量をこれらのベクトル成分に変換するわけですが、材軸方向の力 F は簡単です。材の傾斜角 θ によって { fe } に変換するだけ。 変位量 u1 u2 の方は少々ややこしいので説明は省きますが、これを ( ue1x, ue1y ) および ( ue2x, ue2y ) を使って書き直すことで両者の関係が得られます。 ともあれ、これら一連の操作によって「材軸方向に力 F を受けて ΔL の変形が生じる」状態を全体座標系であらわすことが可能になり、 { fe } = [ Ke ] { ue } の関係が得られます。 この [ Ke ] が 要素剛性マトリクス ですが、参考までに、具体的に書き出すと下の通りです。  ところで、このベクトル { fe } とは何なんでしょうか ? これは「外力」とは違うものですが、しかし、力と変形の関係を得るために「仮想した外力」であると考えることもできそうです。ここではこれを 節点力 と呼ぶことにします。 この用語を使うと、先ほどの式は 節点力 - 変位の関係 です。 さきほどの図に戻りますが、ここにある [ Ke ] の ue2x と ue2y に関わる成分には下線が引かれています。 ここにはもう一つ、右下がりの要素 ( 2 - 3 ) があることを思い出してください。 節点 2 はその要素と共有されている。つまり要素 2- 3 にも ( ue2x, ue2y ) の自由度成分があるので、次の段階でこの要素を全体剛性マトリクス組み込んだ時、その成分の値がここに加算されます。そのことを下線で強調しておいたものですが、ようはこのプロセスが「 要素剛性マトリクスの重ね合わせ」なのです。 さて、このようにして全体剛性マトリクスが出来上がれば、その逆マトリクスと既知の外力ベクトル { f } から変位ベクトル { u } が分かる。そしてこれが分かれば、個々の要素の変位ベクトル { ue } も分かり、そこから節点力ベクトル { fe } が得られる。節点力ベクトルが分かれば ( 上記の逆の手順をたどって ) 要素の「応力」が分かるはず。 ━━というのが変位法のおおまかな流れです。 ここであらためてそれを復習したのは、基本的な流れは対象が「面」になっても変わらない、ということを確認するためですが、ただし、面材に特有のものもあります。それが「応力 - ひずみの関係」です。 有限要素法による一般的な表現 先の「応力 - ひずみの関係」の内容には「手抜き」があります。何かというと、「ひずみ ε は材のどこでも同じ値になる」ことを自明の前提にしている部分です。以下、そのあたりを含め、ここでは有限要素法における一般的な表現を紹介します。 下図の①は、1 端の位置が x1, 2 端が x2 の材の両端にそれぞれ u1 および u2 の変位が生じた状態をあらわしたものです。 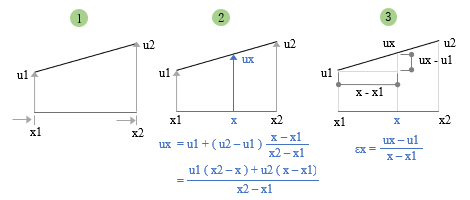 ここでまず最初に、変位量 u1 と u2 を成分にもつ ue = { u1 u2 } というベクトルを考えます。 ( なお、ベクトルはここにあるような「横並び」ではなく、本来は前項の図中にあるような「縦並び」ですが、それを画面にあらわすのは大変なので、文章の中では「横並び」に書くことにします ) 。 図の②は、ここから材の任意位置 x における変位量 ux を求めようとしたものです。 実際の値は図中の式にある通りですが、これを [ N ] というマトリクスを使って ux = [ N ] { ue } と書きます。 この [ N ] は「両端の節点変位から任意位置の節点変位を求める」もので 形状関数 と呼ばれますが、具体的な値を書き出すと ( 1 / L ) [ ( x2 – x) ( x – x1 ) ] です ( ただし L は材の全長 = x2 – x1 ) 。 次に、この位置におけるひずみ εx を求めてみます。これが図の③です。 ひずみは変形量を材の元の長さで割ったものですが、この場合の分母 ( 元の長さ ) は x – x1 。そして「応力-ひずみの関係」に書いたように、変形量は両端の変位量の差なので、分子は ux – u1 です。 ここであらためて図に注目してください。 この分数は u1 から u2 に向かう線分の「傾き」をあらわしたものになっています。そしてこれは直線なので、傾きは位置 x に関係なく一定になる。 x の値と無関係に決まるのです。 これをより一般的に表現すると ひずみとは変位量を距離で微分したもので、ということです。 話を戻しますが、有限要素法では εx を εx = [ B ] { ue } のように書きます。 この [ B ] は 「節点変位からひずみを求める」もので、ひずみ - 変位マトリクス です。 既述のように、[ B ] には位置 x の情報は含まれず、具体的に書くと ( 1 / L ) [ -1 1 ] ですが、この値は、先ほどの形状係数 [ N ] の成分を x で微分したものであることが分かるでしょう。 ひずみ εx は一定なので、これをあらためて ε とすると、ここから応力 σ は σ = [ D ] ε で得られます。 この [ D ] は 「ひずみから応力を求める」もので、応力 - ひずみマトリクス です。 さらに、ここに ε = [ B ] { ue } を代入して σ = [ D ] ε = [ D ] [ B ] { ue } とすると、これが「応力と節点変位の関係」です。 で、それからどうするのかというと、これでようやく要素の剛性マトリクス [ Ke ] が作れるのですが、これについては「その 4」で取り上げることにします。 まとめ ここまではトラス材を中心に書いてきたので、ひずみも応力も成分が一つしかありませんでした。 しかし、面材の場合はここに複数の成分が含まれます。そこで、これを { ε } { σ } のように書き直した上で、あらためて有限要素法の手順を整理しておきます。
 次へ その1 その2 その3 その4 その5 その6 |