|
平面応力 下図左は前項で取り上げた三次元要素を再掲したものです。右にあるのは、三次元要素の z 方向のサイズ ( 厚さ ) が小さい「板」のようなもので、応力についても、やや実状に近い形で描き直しています。 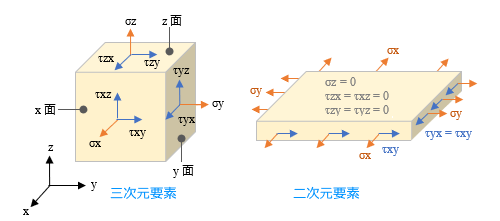 ここで、この二次元要素に対して以下のような条件を設けます。
σz = τzx ( τxz ) = τzy ( τyz ) = 0 となり、さらに τyx = τxy なので、この二次元要素の応力ベクトルの未知成分は最終的に { σx σy τxy } の三つだけになります。これに対応するひずみベクトルの成分は { εx εy γxy } です。 さらに、この場合の節点の自由度成分は ( x , y ) の二つになります。 ここでは最もシンプルな三角形 1 次要素 ( 計 3 節点 ) を考えることにすると、下図のように、この場合の自由度の成分は計 6 個で、節点の変位ベクトルは ue = { ux1 uy1 ux2 uy2 ux3 uy3 } です。 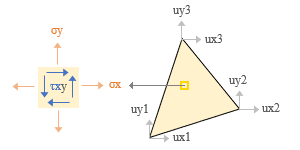 「その 2」の最後に書いたように、要素の剛性マトリクスを作るためには以下の三つの値が必要です。 ・ 形状関数マトリクス [ N ] ・ 応力 - ひずみマトリクス [ D ] ・ ひずみ - 変位マトリクス [ B ] 以下、これらについて順に見ていきましょう。 ● 形状関数 [ N ] これは「節点変位から要素内の任意位置の変位を求める」ものです。 さらに、もしこれが位置の一次関数であらわされるのなら、以後の操作はいたって簡便になるのでした。 任意位置 ( x, y ) の変位量 u, v が位置の一次関数であるとは、具体的に言うと、それが下図中央にあるような式であらわされることを意味します。 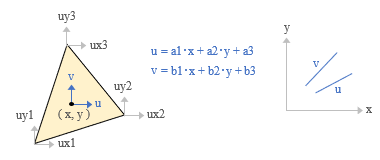 ここにある 6 個の係数 ( a1, a2, … , b1, b2, … ) は求めることができます。要素の頂点にある計 6 個の自由度成分ごとに式を立てれば、6 個の未知数に対して 6 個の方程式ですから━━とは言え、これは要素がたまたま 3 節点 6 自由度だからそうなったのであり、それ以外の場合は保証できないことになりますが、これについては後ほどふれます。 ともあれ、ここから形状関数 [ N ] を作ることができれば、u と v を成分とする任意位置の変位量 { u } は節点変位量 { ue } から { u } = [ N ] { ue } で得られます。 ここにある [ N ] は 2 行 6 列で、以下のような形をとります。n1 n2 n3 の具体的な値については略しますが、いずれも x あるいは y の一次関数です。 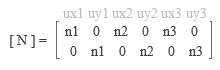 ● ひずみ - 変位マトリクス [ B ] これは「節点変位から要素内の任意位置のひずみを求める」ものです。 ひずみと変位の関係については「その 2」でもふれましたが、線材だったので一つの位置変数 ( 端部からの距離 ) しかありませんでした。 しかし今回は ( x, y ) の二つの変数があるので、任意位置の変位量 u と v に応じたひずみ { ε } の三成分は下のような偏微分 ( もしこの用語と記号に抵抗があるのでしたら「たんなる微分」でも構いません ) であらわされることになります。 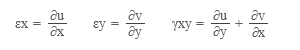 εx と εy は線材と同じで、変位量を距離で微分したものです。γxy については少々説明が必要かもしれませんので、下に図示しました。 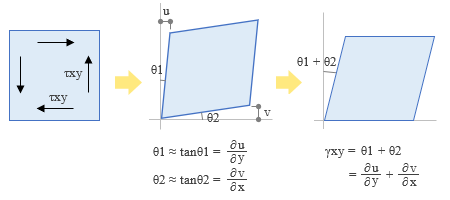 先に書いたように、ひずみ - 変位マトリクス [ B ] とは形状関数 [ N ] を距離で微分したものです。 そこで、先の [ N ] に上の関係を適用すると、3 行 6 列の [ B ] が下のように得られます。  ここにある n1 n2 n3 は x あるいは y の一次関数なので、[ B ] の成分はすべて定数です。 結局、任意位置のひずみ { ε } は節点の変位量 { ue } から { ε } = [ B ] { ue } で求められることになります。 ● 応力 - ひずみマトリクス [ D ] これは応力 { σ } とひずみ { ε } の { σ } = [ D ] { ε } という関係をあらわすもので、以下になります ( E : ヤング係数・ ν : ポアソン比 ) 。 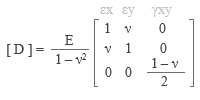 ● 要素の剛性マトリクス [ Ke ] 以上の値をもとに要素の剛性マトリクス ( 節点力 - 変位の関係 ) を作りますが、これには「仮想仕事の原理」を使います。仮想仕事の原理とは 物体が外力の下で釣り合い状態にある時、物体に微小な仮想変位を与えても、物体内に生じる内部仕事 ( 仮想変位によるひずみ × 応力 ) と外力がなす外部仕事 ( 外力 × 仮想変位 ) は等しいというものです。 まず最初に、以下のような節点力ベクトル fe と節点変位ベクトル ue を作ります ( 下図右 ) 。 fe = { fx1, fy1, fx2, fy2, fx3, fy3 } ue = { ux1, uy1, ux2, uy2, ux3, uy3 } さらに ue に対応した微小な仮想変位ベクトル ue* と要素内の仮想ひずみベクトル ε* ( 成分 εx, εy, γxy ) を考えて仮想仕事の原理を適用し、それを変形すると下のようになります。 ━━なお、ここにある二重積分の記号と dxdy は「要素の全面積について積分する」という意味です。また、記号 T は転置マトリクス ( 元のマトリクスの行と列を入れ替えたマトリクス ) をあらわすもの。  上にある式の大部分は忘れてもらって構いませんが、下線がある [ Ke ] ( 要素の剛性マトリクス ) の式だけはおぼえておいてください。 先に書いたように、ここにある [ B ] も [ D ] も ( x, y ) に依存しない定数です。なので、これらは丸ごと積分記号の外に出すことができるはず。そしてこれを外に出してしまうと、この二重積分はたんに要素の面積をあらわすに過ぎません。そこでこれを A とすると、最終的に [ Ke ] = t・A [ B ] T [ D ] [ B ] が得られます ( t・A は要素の体積 ) 。 ここから先の手順は省略しますが、たびたび繰り返しているように、基本的な考え方は「その 2」にある線材のものと変わりません。 ━━ここまで紹介してきたのは二次元平面要素のうちの 平面応力 と呼ばれる問題ですが、ここには別の考え方もあります。参考までに、そちらの方も簡単に紹介しておくことにします。 冒頭に書いたように、平面応力とは板に直交する方向の応力 σz を 0 としたものです。 しかし σz を 0 にしても、この方向のひずみ εz が 0 になるとは限りません。なぜならここには、σx と σy による εz = - ( σx + σy ) ( ν / E ) という関係があるからです。 これに対し、その εz の方を 0 にするという考え方があって、こちらは 平面ひずみ と呼ばれます。 これは「非常に長いものから一断面を切り出した」ような状態で、たとえば土木関連のトンネルの解析などに使われるらしいですが、建築方面で使われることはまずないでしょう。 次へ その1 その2 その3 その4 その5 その6 |