|
四角形要素の応力 前回取り上げた要素の剛性マトリクス [ Ke ] の計算式を下に再掲します。 この [ B ] は「ひずみ - 変位マトリクス」、[ D ] は「応力 - ひずみマトリクス」で、二重積分記号はこれを要素内のすべての位置 ( x, y ) について積分することをあらわしています。 前回の内容は、[ B ] には位置情報 ( x, y ) が含まれないので、これを積分記号の外に出して簡潔な式に変えられる、というものでした。 これは「一つの要素内でひずみ ( および応力 ) は一定である」と近似もしくは仮定することを意味します。 したがって複数の要素がある場合、各要素の応力値が違うので、隣り合う要素が接する辺では応力が不連続になる。そして、その不連続を緩和したいのなら要素分割をどんどん細かくするしかない、ということです。 ところで、ひずみ - 変位マトリクス [ B ] に位置情報が含まれないのは、要素内の位置 ( x, y ) の変位量をあらわす形状関数 [ N ] が ( x, y ) の一次関数だったからです。だから [ N ] を微分した [ B ] から ( x, y ) の項が消えてしまった。 これについては前回書いた通りですが、そこでもふれたように、こういう具合に事が運ぶのは、取り上げたのが三角形 1 次要素 ( 3 節点 6 自由度 ) という最もシンプルなものだったからです。 この考え方を四角形要素にそのまま適用することはできません。この場合、形状関数 [ N ] は ( x, y ) の二次関数になり、そしてこれを微分した [ B ] の中に ( x, y ) の項が残ってしまうのです。 一方、実務においては多くの場面で四角形要素が採用されます。それはこの方が何かと使い勝手がいいからなのですが、ただしここには、上に書いたような問題がある。 ━━それでどうするのか、というのが今回の内容です。 とは言え、これを正面から取り上げると画面を数式で埋めることになり、それはこの文章の本意ではありません。以下にあるのは「大体こんなもの」という内容の紹介であることを最初にお断りしておきます。 さて、冒頭に掲げた式ですが、これをまともに解いて厳密解が得られるかというと、それは ( たぶん ) できません。そこで「数値積分」という方法を使うことにします。 これは解析的に積分値を求めるのではなく、とびとびの位置 ( 積分点 ) での値を求め、それらを元に近似的な積分値を得るものです。その概念を図示したものが下図ですが、ようするに、ここにある f (x1), f (x2)... を求めていけば真の積分値に近づくことができる、という風に考えてください。 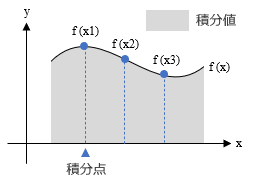 数値積分にもいくつかの方法がありますが、有限要素法では ガウス・ルジャンドル積分 ( 本によっては「ルジャンドル・ガウス積分」となっている ) が使われることが多いようです。ここでは各積分点の値に「重み係数」と呼ばれる値を掛けて集計しています。 積分点の作り方に決まりはありませんが、通常は要素内に 4 個 ( = 2 × 2 ) または 9 個 ( = 3 × 3 ) を等間隔に設けます。下図に示したのは「四角形 1 次要素に 4 個の積分点 ( 青い丸 ) 」です。 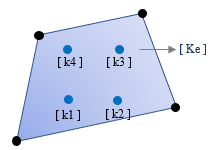 この積分点の位置 ( x, y ) は既知なので、ここから [ B ] を作れば「積分点の剛性マトリクス」が得られます。 途中を省いていきなり結論に行きますが、ここにある 4 個の積分点の剛性マトリクス [ k1 ] ... [ k4 ] に何らかの「重み」を付けて加算すると要素の剛性マトリクス [ Ke ] が出来上がるのです。そういう風に考えておいてください。 さらにこれを全体剛性マトリクスに組み込んで... という、これ以降の手順は変わりません。 ですが、そのようにして要素の変位ベクトルが得られたとして、その後はどうするのでしょうか ? 要素の変位ベクトル { ue } が分かればひずみ { ε } が分かり、それが分かれば応力 { σ } が分かる、というのがここまで紹介してきた解析手順です。しかし今回、ひずみ { ε } は要素内で一定になりません。 そこで、まず各積分点の { ε } を求めることにします。これは変位ベクトル { ue } と積分点の [ B ] から計算できる。そして { ε } が分かれば、これに [ D ] を掛けたものが応力 { σ } です。 この結果、各積分点の応力 σ1, σ2, σ3, σ4 が下図左のように得られます。その後、これらの値を「外挿」という手続きで各節点位置の応力に変換するのです。 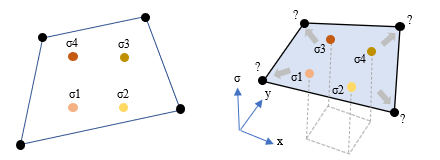 外挿とは 特定の範囲内にある複数の既知の値 ( この場合は積分点の応力 ) から範囲外にある値 ( この場合は節点の応力 ) を予測する数学的な手続きのことです。上図の右から「雰囲気」をつかんでください。 ちなみに、先に登場した形状関数 [ N ] は、これとは逆に、外側の値 ( 節点変位 ) から内側の値 ( 要素内の変位 ) を予測するものでした。こちらは「内挿」と呼ばれます。 本来、応力というのは「要素」に生ずるもので、「節点」ではありません。ですから「節点の応力」と言われてもピンと来ないかもしれませんが、これは上のような手順で得られたものです。「この節点の近辺に生じている応力」と考えておきましょう。 さらに、別の疑問があるかもしれません。 通常、一つの節点には複数の要素が集合しますから、たとえば一つの節点が 3 個の要素で共有されている場合、ここには上のような手続きで得られた 3 個の応力 σ が存在するはずです。そこでどうするのかと言うと、ふつう、これらを平均したものをこの節点の応力にしています。 このやり方はいい加減に思えるかもしれませんが、2 次節点がある場合には、これにより全体の応力分布をなめらかにする効果が生まれるのです。 次へ その1 その2 その3 その4 その5 その6 |