|
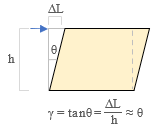
「その 1」に書きましたが、有限要素法の「要素」は、線要素・二次元平面要素・三次元立体要素という風に大別されます。しかしよほどの事がない限り、建築構造方面で三次元要素が使われることはないでしょう。使うとしてもせいぜい二次元の平面要素。 したがって、ここからの話は二次元要素を中心に行いますが、しかし二次元要素というのは、三次元要素の一部を無視して次元を縮小したものです。したがって、まずそこから入る必要があるでしょう。 三次元要素の応力とひずみ 下にあるのは、均等な材質でできた「かたまり」の中から微小な立方体を切り出した状態です ( ここで「微小な」としているのは、その状態では応力が釣り合い状態にあると見なせるからです ) 。この立方体は x 軸に直交する面 ( = x 面 ) y 軸に直交する面 ( = y 面 ) z 軸に直交する面 ( = z 面 ) の三つの面で構成されます。したがって、計 6 面。 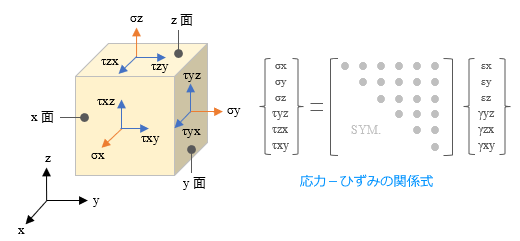 次に、ここに存在する「応力」を見ていきます。 まず考えられるのは、面に直交するもの ( 直応力 ) 。ここでは x 面に作用するものを σx のようにあらわしていますが、同様のものが y 面・z 面にも存在します ( 図中のオレンジの矢印 ) 。 さらに「面内」の応力もあります。 これが「せん断力」で、 τ ( タウ ) の記号を使います。この力は直交する二つの成分であらわされ、たとえば τxy という力は「x 面内に存在する y 方向のせん断力」という意味です ( 図中の青い矢印 ) 。 つまり一つの面に対して三つの応力で、ここには計 18 個の応力があることになります。 しかしこの立方体は釣り合い状態にあるので、向き合った二面の応力の大きさは同じはず。したがって、未知の応力は図中に見えている計 9 個にしぼられます。 さらにもう一つあります。 図を見てもらえれば分かるように、これが釣り合い状態にあるのなら、たとえば x 面の τxy と y 面の τyx の大きさは同じはずです ( でなければ「回転」してしまう ) 。同じことは τxz と τzx、τyz と τzy の関係についても言える。 そういうわけで、求めるべき応力成分は最終的に以下の 6 個にしぼりこまれます。 { σx σy σz τyz τzx τxy } さらに、これらの応力成分に対応するひずみ成分を以下のように定義します。 { εx εy εz γyz γzx γxy } 最初の三成分には ε の記号が使われてますが、これについては「その 2」でふれました。面に直交する応力による要素の「伸び縮み」をあらわしたものです。ただし三次元要素の場合、たとえば εx に関与する応力成分は σx だけではなく、σy や σz も関与することに注意してください ( その度合いをあらわすのが「ポアソン比」という値 ) 。 最後の三成分には γ ( ガンマ ) の記号が使われていますが、こちらは「せん断ひずみ」です。 せん断力 τ と γ の間には τ = G・γ の関係があります。G は「せん断弾性係数」で、ヤング係数 E とポアソン比 ν ( ニュー ) から得られる。 最終的には上図右にあるように、応力ベクトルとひずみベクトルは 6 行 6 列のマトリクス [ D ] によって関係づけられますが、ここでは具体的な値は省略します。 三次元要素の自由度は各節点につき ( x, y, z ) の三成分です。したがって ( 2 次節点を使わない場合は ) 下図にある通り、六面体要素で計 24、四面体要素で計 12 個の自由度になります。 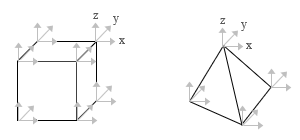 立体要素の話はここまでにしますが、解析の基本的な流れは「その 2」にある線材の場合と変わりません。 蛇足ながら、ここで「せん断ひずみ」という用語が初めて登場したので、少し説明を加えておきます。
次へ その1 その2 その3 その4 その5 その6 |