座屈の理論式
前項で述べたとおり、座屈という現象は様々な要因が複合して起きるものです。なので、その「要因」の方を定量的にとらえて理論化することは難しい。そこでどうするのかというと、「原因はともあれ、軸力が作用して座屈現象が起き、曲がってしまった」状態を出発点にします。
ここでは下図のように、両端ピンの部材に軸方向力 P が作用して曲がっている時、下端から x の位置における力と変位の関係を考えてみます。
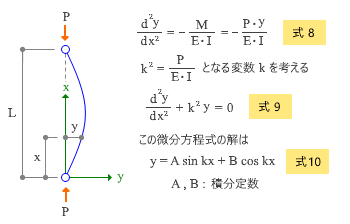
この点の曲げたわみによる横方向の変位量を y とすれば、ここに作用している曲げモーメント M は P・y です。これは一般に非常に小さな値をとるので、通常の応力解析ではこのような二次的な曲げの影響を考慮することはありません。しかし座屈解析においては、この値こそが座屈の原因をなしていると考えるのです。
ここで、以前に紹介した d2y / dx2 = -M / EI という関係 ( ここでは曲げモーメントの向きを考えて右辺に負符号をつけている ) に上記の M = P・y を代入したのが 式-8 で、さらにこれを k2 = P / EI となるような新たな変数を設けて書きなおしたのが 式-9 です。
このあたりの手続きについて説明できる能力は私にはありませんので、興味のある方はご自分で調べてください。とにかく、この 式-9 の微分方程式を解くと 式-10 の解が得られるのです。
ここにある定数 A 及び B は積分定数で、境界条件によって決まります。
まず部材下端における既知の条件として「 x が 0 の時に y は 0 になる」があります。
この場合、右辺第1項は ( sin 0 = 0 なので ) 0 になり、第2項は ( cos 0 = 1 なので ) B になる。左辺は 0 なので、ここから B は 0 でなければならないことが分かります。これでとりあえず、式-10 は
y = A sin kx
と書けることになる。
さらに、部材上端における条件「 x が L の時に y は 0 である」を導入します。
上の式を見れば明らかな通り、この条件が満たされるのは「 A が 0 である」場合と「 sin kL が 0 である」場合の二つしかありませんが、「 A が 0 である」は明らかに私たちが求めている解ではないでしょう。なぜなら、A も B も 0 ならば y はつねに 0 になり、座屈による曲がりは生じないはずだから。
以上から、私たちが求めている解は
sin kL = 0
であることが分かります ( この時 A は任意の値をとり得る、つまり不定 ) 。
さて、上の条件が満たされるケースは複数あります。それは
kL = π, 2π, 3π, ... = nπ ( n は正の整数 )
です。そこで、ここから得られる k = nπ / L を使うと下の 式-11 と 式-12 が得られます。
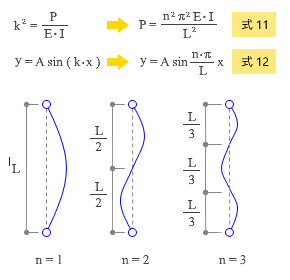
式-12 が教えている通り、部材の変形曲線はサインカーブを描くのですが、ここで n の値を「 1, 2, 3, ... 」と変えた時の曲線を上の図にあらわしました。
このうち、最も単純な変形が上の図の一番左側、つまり n = 1 の時のものであり、この時に荷重 P は最小値をとります。したがって、これが私たちが求めている解であると考えて差支えないでしょう。
この P が部材の「座屈荷重」で、これをさらに部材断面積 A で割ったものが座屈応力度 σ です。
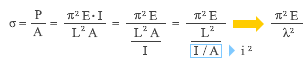
上にあるのは、この式の分母と分子を I で割り、さらにここに断面2次半径 i を導入して i2 = I / A の関係を使って変形したものです。さらに、これを細長比 λ の値を使って書きなおすと前項で紹介した 式-6 になります。
そしてこの σ を降伏応力度 σy に置き換え、細長比 λ を逆算したものが 式-5 の限界細長比 Λ である、というわけです。
ここでは最も単純な「両端ピン」の部材について説明したので、上記の L は部材長そのものになりますが、端部の境界条件が違ってくれば微分方程式の形も違ってきます。その場合の L は部材長そのものではなく、これに何がしかの係数を掛けた「座屈長さ」という値が使われるのですが、そのあたりは学会の規準に定められている通りなので省略します。
( その4 終わり )
前へ | 1 | 2 |
|