剪断応力度と断面設計
前回述べた通り、長方形断面の形状係数は 1.5 です。したがって、曲げと剪断力が作用しているコンクリートなり鉄なりでつくられた長方形部材の剪断力に対する検証は以下の式で行われなければなりません ( fs は許容剪断応力度、Q は設計剪断力、b は断面の幅、D は断面のせい ) 。
fs ≧ τ = 1.5・Q / ( b・D )
しかし、実際に上のような検定式が使われることはないでしょう。鉄板がそのまま部材に使われることはほとんどないし、また無筋コンクリートがそのまま部材として使われることもほとんどないからです。
そこで以下では、「実際にはどのような計算が行われているのか」を見ていくことにします。
最初は鉄骨部材の代表格であるH形鋼です。
この τ の分布は下図中央に示したようなものになります――前項の 式-5 により計算できる――が、一見して分かるように、ほとんどの面積をウェブ部分が占めています。そして図心軸で最大値をとるとはいうものの、ウェブの上下端における値とそんなに大きな違いは見られません。
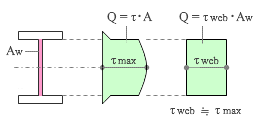
そこで設計上の便法としてとられているのが、「フランジ部分は無視し、ウェブのみが剪断力を負担する」と仮定する方法です。これを図の右に示しましたが、このような仮定に基づいた τweb と τmax の値は「だいたい同じ」になります。その「だいたい」がどれくらいなのかが気になる方のために、いくつかの断面について τmax と τweb の比を試算した表を下に掲げておきました。
| 断面サイズ |
τweb / τmax |
| H-300×150×6.5×9 |
0.933 |
| H-500×200×10×16 |
0.937 |
| H-700×300×13×24 |
0.951 |
次は「鉄筋コンクリート」の話ですが、日本建築学会の計算規準によれば、部材の剪断耐力は「コンクリートの耐力」と「鉄筋 ( 剪断補強筋 ) の耐力」の和としてよいとされています。
ここで取り上げるのはもっぱら前者の方ですが、この耐力 Qa は以下の式で求めることになっています ( j は応力中心間距離、d は有効せい = 圧縮側のコンクリート縁から引張鉄筋の重心位置までの距離 ) 。
Qa = b・j・fs ただし j = ( 7 / 8 ) d としてよい
長方形断面の剪断耐力を求めているわりには、なぜかここに「形状係数 1.5 」は登場しません。あるいはもしかすると、ここにある ( 梁せい D を実質的に低減することになる ) 7 / 8 という係数がその代役を果たしているのでしょうか?
そのように考えられないこともないですが、しかしやっぱり、違うでしょう。以下はそのあたりの説明です。
下図にあるのは、さきほどと同様に長さ dx の鉄筋コンクリート製の梁断面を取り出し、左右の曲げモーメントの大きさが違っている状態をあらわししたものです。
ご存知の通り、鉄筋コンクリートという複合材は「圧縮力をコンクリートで負担し、引張力を鉄筋で負担する」という分業で成り立っています。したがってこの時、曲げモーメントの差 dM によって生じる応力度は、鉄筋についてはオレンジ色の矢印の長さ、コンクリートについてはオレンジ色に塗りつぶした面積であらわされます。
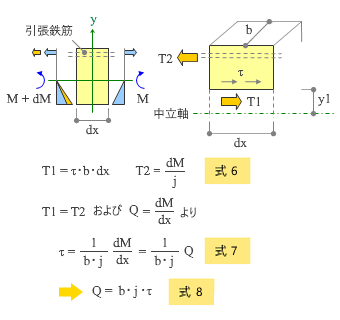
ここでさきほどと同様、中立軸――その位置は、鉄筋の引張力とコンクリートに生じている圧縮応力度の合力から求められる――から y1 の位置で水平方向に切り出した断片を考えることにしましょう。
剪断応力度 τ によって生じる力 T1 の値はさきほどと同じ。さらに、鉄筋の引張応力度の差に相当する力 T2 とは、曲げモーメントの差 dM によって生じる応力度ですから、式-6 にある通り、dM / j という値をとります。
この両者を等置し、Q = dM / dx の関係を使って書き直したのが 式-7、さらにこれを変形したのが 式-8 です。
お分かりのように、先ほど紹介した剪断耐力 Qa の式とは、式-8 の τ をその上限値である許容剪断応力度 fs に置き換えたものです。
( その3 終わり )
前へ | 1 | 2 | 3 | 4 |
| 
