「たわみ」と「たわみ角」
前回求めたのは梁の「回転角」の値です。しかし、「そんなものを求めてどうするのか」と思われた方も多いかもしれません。多くの場合、直接問題になるのは「たわみ」= 鉛直方向の変位量の方でしょう。しかし前回の図の中に、それを求めるためのヒントがすでに隠されていたのです。
前回の図を下に再掲しますが、今度は、材軸方向に沿った x 軸に加え、これに直交する y 軸 ( 鉛直方向の座標軸は通常「上向きが正」になるが、ここでは変位が下向きに生じるので、話を分かりやすくするために「下向きが正」にしている ) も考えることにします。
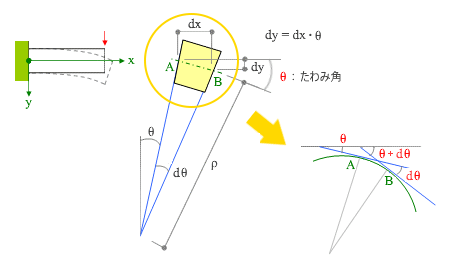
前回取り上げた回転角 θ とは、ここにあるような「変形後の切断面が鉛直軸となす角度」のことでした。しかしこの変形により、( もともと水平だった ) 梁の重心軸にも何らかの傾きが生じることになる。これが上の図に赤い文字で書き入れた θ です。これを たわみ角 と呼んでいます。
ただし、実際にはもう少し複雑です。部材の重心軸は「直線」ではなく、変形後に「円弧」になるからです。
このあたりを説明した拡大図が上図の右ですが、ここにあるように、「 A 点を通る円の接線が水平軸となす角度」が θ で、「 B 点を通る円の接線が水平軸となす角度」が θ+ dθ になります。
ここで例によって「 θ が微小であれば」という仮定をとることにより、θ と dy の関係は上図の四角で囲んだ式であらわせますが、これを再掲したのが下の 式-4、さらにこれを変形したのが 式-5 です。
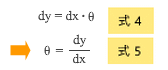
ここで dx を 1 にすれば θ は y の値そのものになる。つまり、
たわみ角とは単位長さあたりの変位をあらわしたたもの
なのです。
この点についてもう少し具体的に考えてみましょう。
下のグラフは距離 x と変位 y の関係を示したもの――さきほどと同様、本来は θ と y に関してその「正負符号」を問題にしなければならないのですが、ここでは気にせずに話を進めています――ですが、y が x と比例して増加するのであれば、この関係は直線になります。そして 式-4 から明らかなように、たわみ角 θ がこの直線の傾きになる。これが左側のグラフですが、言うまでもなく、このような状態になるのは「曲げモーメントが一定で、全長にわたって部材が同じ曲率で変形している」場合です。
これに対し、もし曲げモーメントが変化しているのであれば、この関係は何らかの「曲線」で表わされるはずですが、これが右側のグラフになります。そしてある点におけるたわみ角 θ とは、この曲線に引いた接線の勾配に相当するのです。
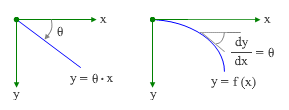
念のために補足しますと、右のグラフにある y = f ( x ) の式は「 y の値が変数 x の関数になっている」ことを意味するものです。しかし、私たちはまだこの関数の正体を知りません。このグラフを完成させるには θ を x の関数であらわし、変数 θ を消去する必要があります。
ここで使うのが前回紹介した曲率と回転角の関係 ( 式-1 )、及びそこから得られた曲げモーメントと回転角の関係 ( 式-2 )です。これを下に再掲し、ついでに 式-2 を変形した 式-2’ も書いておきます。
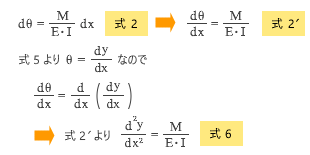
式-2’ と 式-5 ( θ = dy / dx ) を見比べてください。式-5 の θ を x で微分したもの、つまり微小区間 dx におけるたわみ角の増分が dθ なのです。これは dy / dx をもう一度 x で微分することにほかなりません ( これを d2y / dx2 のように表記する習慣がある ) 。
結局、式-6 の微分方程式こそが私たちが求めていたものなのでした。
これを1回積分すると dy / dx ( = たわみ角 θ ) が x の関数になり、さらにこれをもう1回積分すると y ( = 変位量 ) が x の関数になるのです。
これが最終的にどのような形をとるかは曲げモーメント M がどのように分布するかに依存します。ちなみに、これが直線的に変化する ( たとえば先端に集中荷重を受ける片持ち梁のようなもの ) 場合は θ は x の2次関数、y は x の3次関数になります。
( その2 終わり )
前へ | 1 | 2 |
|