1.　断面2次モーメントと曲げ剛性
2.　曲げモーメントと曲げ変形
3.　剪断力と剪断変形
4.　座屈
5.　横座屈

前回の冒頭で「意味のよく分からない式」の代表格として「座屈を考慮した許容圧縮応力度」を取り上げましたが、それに輪をかけてよく分からないのは「横座屈を考慮した許容曲げ応力度」です。圧縮力を原因として起きる座屈現象を説明する際、よく「アクリル製の物差しを両手に持って縦に押し込んでみると...」という喩えが使われますが、しかし「曲げを原因として起きる横座屈」を身近に体験するのは難しい。
というわけで、まずは「横座屈とはそもそも何なのか」から話を始めることにします。

「曲げ」と「捩れ」

前回取り上げた座屈は圧縮力を原因として起きるものなので「圧縮座屈」あるいは「オイラー座屈」と呼ばれます。また、その結果として部材が「曲がる」ので、「曲げ座屈」という呼ばれ方をすることもあります。
これに対し、横座屈は「曲げ捩 ( ねじ ) り座屈」と呼ばれます。
これは部材が「曲がって、なおかつ捩れる」状態を指しているわけで、どちらかというと、こちらの名前の方が端的で分かりやすいような気がします。それにしても、なぜこんなことが起きるのか？
一般には以下のように説明されています。

H形鋼のようなものに曲げモーメントが作用すると、一方のフランジには圧縮力、もう一方のフランジには引張力が発生するが、この圧縮力がある値を超えると座屈を起こす。
しかし断面全体が単純な圧縮力を受けているわけではないので、片側のフランジが座屈によって曲がろうとしても、断面全体はこれに抵抗しようとする。これらの力のせめぎ合いにより、全体として断面が捩れ、横方向にはらみ出すように変形する。これが横座屈である。

たしかにそうなんでしょうが、しかし前回書いたように、「圧縮力による座屈」という現象の直接の原因を特定するのは難しい。したがって上の説明も「なぜそういうことが起きるのか」を教えてはくれません。そもそも、「完全にまっすぐ」で「完全に均質」な部材の重心位置に正確に荷重が作用しているのであれば、横座屈のような現象は理論的には起こり得ないのです。

前回述べたように、部材には必ず何がしかの「元たわみ」が存在します。だから、そのような部材を柱に使うと、それが一因となって座屈が起きる。では、そのような「曲がった材」を梁に使ったらどうなるか、ということを考えてみたのが下の図です。
　　
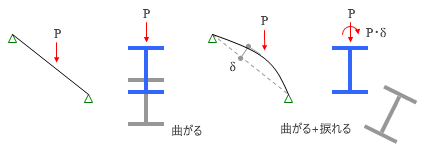
これはH形鋼の単純梁のウェブ軸に沿った方向に鉛直荷重 P を加えた状態ですが、この部材に元たわみがなく完全にまっすぐであれば、この梁には「曲げモーメント」と「剪断力」という力しか生じません。そして梁は鉛直方向に曲がる。これが図の左側の状態です。
これに対し、右側にあるのは、梁に δ という水平方向の元たわみがある場合です。
この時、梁には P に加えて P × δ という大きさの「捩りモーメント」も作用するはずです。これにより、梁は鉛直方向に曲がると同時に部材の中心軸回りに捩れることになり、これらの変形が合成された結果、梁は横にはらみ出すような変形をしてしまう。たぶん、これが横座屈という現象の説明としては一番分かりやすいと思うのですが、どんなものでしょうか？

ちょっと話がそれますが、「座屈以外の理由でも部材は捩れる」という話題を先に取り上げておきます。
捩りモーメントが作用しているH形鋼の断面には、下図左に示すように、上下のフランジ断面に材軸に直交する剪断力が発生し、これが何らかの偶力モーメントを形成して外力と釣り合っているはず。これは間違いないでしょう。
　　
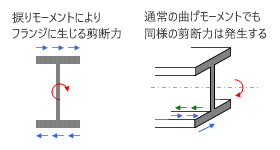
しかしこのような種類の剪断力は、捩りモーメントが作用していなくても、つまり「ふつうの曲げモーメント」が作用している状態でも存在しているものなのです。しかし、にもかかわらず、「ふつうの曲げモーメント」によって断面が捩れることはない。それはなぜなのか、ということを考えてみます。

先に「剪断変形」の項で説明したように、曲げモーメントの変化による剪断力とは、曲げモーメントによって生じる引張り ( あるいは圧縮 ) 応力度の差によって部材が軸方向に「ずれようとする」ために発生します。
H形鋼のフランジの片側部分だけを考えてみると、その一端には何の拘束もなく、別の一端はウェブによって拘束されています。したがって上図右にあるように、この「ずれようとする力」はフランジとウェブの接合部分に集約的にあらわれてくるはずです。
ところで、これも先に述べた通り、剪断応力度は必ず「ペア」で存在するので、この応力と釣り合いを保つべき応力がその直交方向、つまりフランジの横断面上に存在していなければなりません。これがさきほど述べた「フランジに生じているはずの剪断力」です。

容易に想像できるように、この剪断力はフランジの自由端で 0 になり、ウェブとの付け根部分で最大になります。ウェブを境にした反対側のフランジでも同様ですが、ただしこの場合は応力の向きが逆になる。そして上側のフランジと下側のフランジでは ( 曲げによるフランジの引張り・圧縮の違いにより ) これまた向きが逆になります。
結局、H形鋼に生じている剪断応力の「向き」と「大きさ」を勘案してその分布を表わすと、下図左に示したようなものになります。中央には「剪断変形」の項で説明した「H形鋼の剪断応力の分布」の図を再掲しましたが、ようするに、これをさらに仔細に見てみると左側のようになっている、ということです。
　　
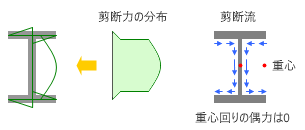
さて、左側の図をよく見てみると、上フランジの先端で 0 になっている応力がウェブの付け根に向かって大きくなり、それがウェブに伝わって、さらに下フランジの付け根から先端に向かって小さくなり、先端で再び 0 になる。つまり右側の図に矢印で示したように、あたかも剪断力が上フランジの先端からウェブを伝って下フランジの先端まで「流れて」いるように見える。そこで、これには 剪断流 という名前がつけられることになりました。 ^{注 )}

注 )
ただしこの考え方は鉄骨部材のような「薄肉断面」に対してのみ適用さます。このようなものでは、剪断力が肉厚の中心軸に沿って流れると考えた方が実状に合うことが分かったのです。

で、ここで何を言いたいのかというと、右側の図の矢印を見てもらえば分かる通り、H形鋼のような対称断面――正確には2つの対称軸をもつ「2軸対称断面」――では、左右のフランジの剪断応力が逆向きに生じるため、これらが結果的に打ち消し合い、重心回りの偶力モーメントは生じないことになる。だから「まっすぐなH形鋼の重心軸方向にまっすぐに力を作用させれば断面が捩れることはない」のです。
しかし、これはあらゆる形状の断面に当てはまるわけではありません。溝形鋼――対称軸が1つしかない「1軸対称断面」――の剪断流を下に図示してみました。
　　
この断面の重心回りの偶力モーメントを考えてみると、まずフランジの応力による反時計回りの曲げが発生し、さらにウェブの応力によって同様に反時計まわりの曲げが発生します。その結果、ここでは「重心位置に荷重をかけても断面が捩れてしまう」のです。

話の順序が逆になりましたが、実は、このような断面がなぜ捩れてしまうのか、という疑問から出発し、それを合理的に説明するために剪断流という考え方が生まれた ( らしい ) のです。しかし、それはともかく、この断面が捩れないようにするには重心位置に力を作用させてはいけません。ではどの位置に作用させればいいのかというと、それは上の図から明らかでしょう。
ウェブの応力による曲げが時計回り ( フランジによる曲げと反対向き ) になるような位置、つまり断面の外側に作用させればいい――もっとも、そのためにはウェブから「腕木」のようなものを出しておく必要がありますが――のです。この位置が 剪断中心 と呼ばれるもので、形鋼のテーブルなどにはたいてい載っています。

このような1軸対称断面の「捩れ」をはたして「座屈」と呼んでいいのかどうかは難しいところですが、しかしこれから見ていくように、建築学会の計算式やその解説等でもこれらを一括して「横座屈」という範疇に入れているようです。