振動解析の基本用語

振動という現象の最大の特徴は「周期性」がある、つまり「一定の時刻ごとに同じ現象が繰り返される」という点にあります。そして、その最もプリミティブな形態は「円周上を等速で移動する質点」によって表わされ、これは 調和振動 あるいは 単弦振動 などと呼ばれます。下図を見てください。

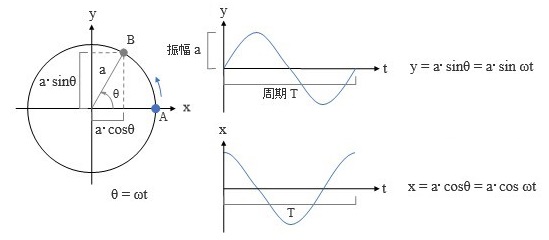
図の左にあるように、半径 a の円周上の A にある質点が B に向かって反時計回りに移動しているものとします。この質点の y 軸上の位置、及び x 軸上の位置を時間軸 t に沿って表したものが右上及び右下のグラフです。右上を「サインカーブ」、右下を「コサインカーブ」と呼ぶことは今さら説明するまでもないでしょう。
また、これまたご存じの通り、コサインカーブとサインカーブは始まりの位置が 90 度ずれている――これを「位相 がずれている」という――だけで、波の形は同じです。なので、以下の説明にはもっぱらサインカーブ ( 正弦波 ) の方を使うことにします。

この波形の高さ ( の絶対値 ) は半径 a になります。これが 振幅 です。
この質点は円周を一周すると元の位置に戻り、以後は同じ軌跡を繰り返すわけですが、この 1 サイクルに要する時間 ( 秒 ) が 周期 T です。この逆数は「 1 秒の間に生起するサイクル数」になりますが、こちらは 振動数 あるいは 周波数 と呼ばれ、ヘルツ ( Hz ) という単位で表わすことになっています。
ところで、質点が円周上を一周する 1 サイクルとは、左側の図中に示した角度 θ が 0 から 360 度 ( ラジアン単位で 2π ) まで変化することに他なりません。そして、その 1 サイクルに要する時間が周期 T なのですから、結局、質点が単位時間あたりに移動する角度は 2π / T になる。これが 角速度 で、ギリシャ文字の ω ( オメガ ) という記号をあてる習慣があります。
この値を使うと角度 θ は ωt なので、図の右上にあるように、変位 y は a・sin ωt と表わせることになります。この表現は振動理論にたびたび登場するので是非覚えておいてください。
角速度 ω ・周期 T ・振動数 f の関係を下にまとめておきましょう。

　　 ω = 2π / T = 2π ・ f　　( f = 1 / T )

話を戻しますが、上に述べたのは円周上を「等速」で移動している質点です。ここで「加速度とは速度の変化率である」という定義を思い起こすと、この運動には加速度がまったく関与していないように錯覚しそうですが、もちろん、そんな筈はありません。
私たちがいうところの「速度」とは円周の接線方向に向かうものを指すわけですが、下図に見るように、時間が ��t だけ経過した ( = 角度が ω��t だけ変化した ) 後にはその「向き」が変わります。
動く向きが変わるのはそこに何らかの「力」が作用しているからで、したがってここには「加速度」が存在するのです ( その力が質点を円周上に留めていることになるので「向心力」と呼ばれる ) 。

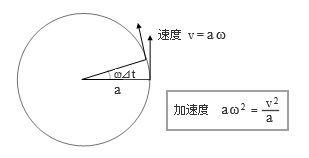
詳しい証明は省きます――たぶん高校の物理の教科書あたりに載っているはず――が、ここには上式のような大きさの加速度が作用していいる、ということだけを頭に入れておいてください。
じつは、この式を使って「関東大震災の地動加速度」を計算した人がいたのです。

関東大震災が起きた 1923 年当時、東京大学の構内に地震計が設置されていました。と言っても、当時の地震計はカーボン紙を針で引っ掻いて揺れを記録する「変位計」と呼ばれる単純なものだったようですが、揺れがあまりに激しいために壊れてしまった。
そこで、壊れる直前の波形を読み取ってみると、全振幅 ( 振幅の 2 倍 ) が 88.6mm、周期が 1.35 秒でした。これさきほどの式に当てはめると、この地震の加速度は
　　　 ( 88.63 / 2 ) × ( 2π / 1.35 ) ² = 970 mm/sec²
なので、地震動の大きさは約 0.1G であったと考えられる――これは、棚橋諒博士の 1935 年の論文「地震の破壊力と建築物の耐震力に関する私見」にあるものです。もろもろの事情を考えると、この数字にどこまでの信頼性があるのかは疑問ですが、「地震を単弦振動と見なせば、その波形から加速度を求めることができる」ことの一つの例として紹介しました。
しかし言うまでもなく、実際の地震動は単純なサインカーブで表せるものではありません。