安全限界時の検証 ( 2 )

建物の各階の必要累積塑性変形倍率と保有累積塑性変形倍率を比較し、前者よりも後者が大きければよい、というのが前回の話でした。今回の話は、後者の「保有累積塑性変形倍率」のもとめ方です。
ところで私たちは、ある階の保有累積塑性変形倍率の値は知りませんが、各部材の保有累積塑性変形倍率の値なら知っています。と言っても、これは鉄骨造の部材に限った話ですが、保有水平耐力計算で使う部材種別の区分は「保有累積塑性変形倍率」の値にもとづいて行われているのです。ちなみに、FA 部材が保有する累積塑性変形倍率は、柱については 6、梁については 3 になります。^注）

注）
この累積塑性変形倍率は、鉄骨部材の「局部座屈」による耐力低下をもとに決められたもので、圧縮座屈や横座屈、あるいは接合部の破壊等が起きないことが前提になっています。したがってエネルギー法の場合も、たとえば保有水平耐力計算の規定にしたがうなどの配慮により、これらのリスクをあらかじめ排除しておく必要があります。

そうなると問題は、各部材の保有累積塑性変形倍率を、どのようにしてその階の保有累積塑性変形倍率に変換するか、になりますが、前者を mηu、後者を rηu という記号であらわすと、ここには以下のような関係があるとされています（この式を導くための前段があるのですが、省略して結果だけを書きます）。

梁の場合　　rηu = mηu + 2.0
柱の場合　　rηu = ( 5 / 6 )×mηu + 2.0

さらにここで、下図にあるような「層ユニット」と呼ばれるモデルを導入します。

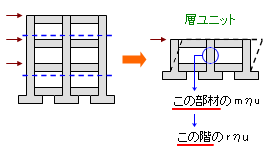
これは、建物を構成する特定の階だけを切り出して平屋の建物に擬したものですが、この階全体の性能は、この「層ユニット」を構成する部材の性能によって決定されると考えるのです。
そこで、ここに含まれる部材の累積塑性変形倍率 mηu をもとめ、さらに上の式によって、mηu から定まるその階の累積塑性変形倍率 rηu をもとめます。そして、すべての部材から得られる rηu のうち最小値を「その階の保有累積塑性変形倍率」とするのです。
これによって得られる解の精度がどの程度のものなのか、については私は分かりません。しかし、非常にスマートな考え方であることはたしかです。

たとえば限界耐力計算の場合を考えてみます。
ここで言っている結論は、「安全限界耐力（限界値）が必要安全限界耐力（応答値）よりも大きければよい」というものでした。しかしご存じのとおり、ここでは「安全限界耐力（限界値）」が分からない限り「必要安全限界耐力（応答値）」が分からない仕組みになっています。そのため、どうしても、「試行錯誤を重ねて解を収束させる」という作業が必要になってきました。
それに対し、ここまで見てきたように、エネルギー法では「限界値（保有累積塑性変形倍率）」と「応答値（必要累積塑性変形倍率）」をもとめる手続きが独立しています。つまり、目標とすべきものが最初から見えているのです。さきほど、「スマート」と形容したのはこのことを指しています。

ところで、ここまで見てきたのは、もっぱら鉄骨造の建物の場合です。なぜエネルギー法が「累積塑性変形倍率」という考え方を採用しているのかというと、一つには、最初に話したような「履歴ダンパー」の性能をあらわすのにこの考え方が最も適合していること、そしてもう一つは、鉄骨部材の累積塑性変形倍率という値については多くのデータの蓄積があったことでしょう（あくまで私の推測に過ぎませんが、たぶん、そういうことなのだと思います）。
だからエネルギー法は鉄骨造の建物と非常に相性がいいのですが、その一方、コンクリート系の建物の方をどうするか、という問題が残ってしまいました。

こちらについては、「累積塑性変形倍率」に関するデータがほとんどないのです。かわりにあるのが「塑性率」です。そこで仕方なしに、「累積塑性変形倍率を塑性率に換算する」という方法をとることにしました。

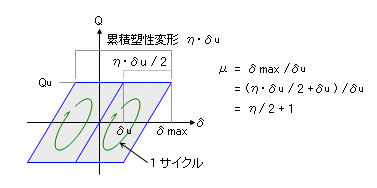
上に累積塑性変形の概念をあらわす図を再掲しましたが、塑性率とは、その階の最大変位 δmax を降伏時変位 δu で割った値です。ここにあるように、正側の最大耐力 Qu+ に達した後 δmax まで変位が進み、その後に力の向きが変わって負側の最大耐力 Qu- に達してから原点に戻ってくるまでを変形の「 1 サイクル」と考えると、ここにある累積塑性変形によるエネルギー吸収の総量は、塑性率で考えた場合の「 2 サイクル」に相当します。その結果、塑性率 μ（ミュー）と累積塑性変形倍率 η はここにあるような式で関係づけられることになります。
そこで、この関係式を使って、「必要累積塑性変形倍率」を「必要塑性率」に変換してしまうのです。それはそれでいいのですが、問題は、「保有累積塑性変形倍率」に対応する「保有塑性率」とでもいうべき値をどのようにもとめるか、の方でしょう。

すぐに思いつくのは、「保有塑性率」とは建物の安全限界状態そのものを指していることになるので、それならば、限界耐力計算と同様に「増分解析」によって安全限界状態をもとめればいいではないか、というアイディアです。実際、「計算例と解説」ではそのような方法をとっています。
ここにある手順をそのまま紹介しておきますと、まず最初に「安全限界状態の層間変形角」を決めてしまい、とにかくその状態になるまで建物を押して行きます。そして、その状態においてすべての部材に耐力低下が起きていないことが証明できれば、それを建物の安全限界状態と考えて構わない（本当の安全限界状態ではないかもしれないが、しかし、それ以下であることは保証される）という立場をとるのです。その時の塑性率が「保有塑性率」になります。

しかし、この例題にあるのは、均一なプランと剛性を持った、理想的な全体崩壊メカニズムを形成する建物です。つまり、各階の保有水平耐力の分布が「 Ai 分布による層せん断力の分布」と相似になり、結果的に、各階の pi がほとんど 1 に近い値になっています。
だから、増分解析時に「 Ai 分布にもとづく外力分布」を作用させることに何の問題もないのですが、そうでない建物の場合は、どのような外力分布を作用させるべきかで悩むことになりそうです。
いずれにしても、コンクリート系構造物に対するエネルギー法の適用については「発展途上段階」と考えておいた方がいいのではないでしょうか？

--- 終わり ---
（文責　　野家牧雄）