|
その理由は、おそらく、
そこで今回は、これまでいただいた質問等を参考にしながら、擁壁の設計のポイントについて復習してみることにしました。 土圧の種類 土圧とは、鉛直方向に自重 ( あるいは地表面の載荷重 ) が作用している土塊に生じる水平方向の応力成分です。この値は土の深度が大きい、つまりその点から上方にある土の重量が大きくなるほど大きくなる。土圧係数 とは、この時の土の重量と土圧の大きさを関係づける比例定数で、土圧力 P ・ 土の重量 W ・土圧係数 K の間には以下の関係があります。 P = K ・ W 下図のように、壁の片面に土が盛られ、壁の下部に何らかの回転バネが付いた状態を考えてみます。このバネが壁の「回転抵抗」を表わします。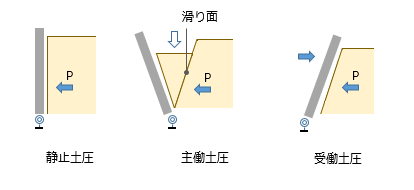 土圧を受けても壁が回転せず、作用土圧力と壁の抵抗力が釣り合っている状態が上図左で、この時に作用する土圧を表わすのが 静止土圧係数 です。 これに対し、図の中央にあるように、回転抵抗が小さい場合は壁が土圧の作用方向に倒れてしまいます。壁が倒れるということは、地盤内に何らかの「滑り面」が生ずる、ということです。 この「滑り」が生ずる直前に作用している土圧の大きさを表わすのが 主働土圧係数 です。 これとは逆に、図の右のように、壁の側に何らかの力を加えれば土はそれを押し返そうとする。この時の土圧の大きさを表わすのが 受働土圧係数 です。 これらの間には 主働土圧係数 < 静止土圧係数 < 受働土圧係数 という関係があります。となると問題は、「擁壁の設計にはどの値を使うのか」です。 私たちは、作用する土圧に対して釣合い状態にある擁壁の応力を求めようとしています。だから当然、ここで使うのは「静止土圧係数」だろう、という風に考えます。ところがそうではなく、実際には「主働土圧係数」が使われるのです。 前述の通り、この値は静止土圧係数よりも小さい。となると、私たちは「危険側」の設計を行っていることになるのではないか。 ――というのが、じつは、私自身の昔からの疑問だったのですが、そこで今回、その理由をあらためて調べてみたところ、どうも以下のような事情らしいです。
土圧係数の値 主働土圧係数を求める計算式として有名なのは クーロン式 で、現在の実務設計ではほとんどこれが使われていると考えて間違いありません。これに対し、手計算の時代には、式の簡便さから ランキン式 というものがよく使われました。これは、一定の条件 ( 地盤に傾斜がない ・ 壁面の摩擦がない ) のもとでクーロン式を簡潔に表わしたものですが、土圧係数というものを概括的に捉えるにはこれの方が適していると思うので、下に掲げておきます。 K = tan2 ( 45 – φ / 2 ) ここにある φ は 内部摩擦角 ( 度 ) です。この値の詳細は次項で取り上げますが、「原則として土質試験により求めること」とされています。しかしながら、なかなかそうもいかない事も多いので、日本道路協会「道路土工 – 擁壁工指針」 ( 以下「道路土工指針」 ) では、背面地盤 ( 裏込め土 ) の性質に応じて下表のような値を使ってもよい、としています。
実際の工事で使用される裏込め土は、上の分類でいう「礫質土」、あるいはそれと「砂質土」の中間のようなものになるでしょう。したがって実務設計では、内部摩擦角の値を 30 ないし 35 度としますが、安全側をとって30 度とすることが多いかもしれません。 一方、「宅地造成等規制法」 ( 以下「宅造法」 ) と呼ばれる法律もあります。ここでは、「小規模の擁壁で、かつ背面地盤が水平なもの」という条件付きで、以下のように土圧係数を直接定めています。
ここにある土圧係数の値は「道路土工指針」に定める内部摩擦角の値をランキン式に当てはめ、さらにそれを安全側に丸めたものと考えておいて間違いないでしょう。両者における「単位体積重量」の値に開きがありますが、これは両者の土質分類の微妙な違いによるものなのでしょうか ? ( そのあたりはよく分かりません ) 内部摩擦角 これは せん断抵抗角 とも呼ばれ、ようするに、土の強度 ( せん断強度 ) を表わしたものです。それなのに単位が「角度」になっているのが不思議ですが、これは土の強度が土粒子間の「摩擦」によって保証されると考えるからで、さらに、「摩擦力を角度によって表わす」という昔からの習慣があるからです。下図のように、角度をつけた板の上にある物体が載っている状態を考えます。この物体と板の間には摩擦力 F が働くため、一定の角度までは滑り出すことがありません。 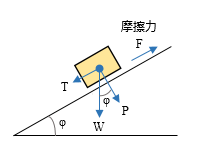 ここで、摩擦力 F は物体の重量 W の斜面に対する鉛直方向成分 P に比例するものと考え、この比例定数を摩擦係数 μ とすると、力の釣合いから以下の式が得られます。 F = T = μ P = P tan φ 話を「土」に戻します。対象となる地盤を何らかの方法で少しずつ傾けていった状態 ( もちろん、そんなの無理ですが、あくまでも概念上の話 ) を想像してください。すると、ある時点で土は安定を保てなくなり、「土砂崩れ」が起きるでしょう。その時の角度が「土の内部摩擦角」なのです。この話は多少乱暴で不正確ですが、大雑把にいえばそういうことになります。 以前、弊社のプログラムのユーザーから「裏込め土の内部摩擦角が 30 度で傾斜角が 35 度」というようなデータが送られてきたことがありますが、そういう状態は「あり得ない」ということが上の話から分かっていただけるでしょう。 ただし、これはあくまでも「理論上」の話です。 土の強さを構成するファクターには、この他に「粘着力」というものがあるので、それを考慮すれば、傾斜角が内部摩擦角を超えてもただちに崩壊するわけではありません。が、通常の設計では「粘着力の項は無視する」という立場がとられます。 壁面摩擦角 内部摩擦角とは、文字通り土の「内部」、つまり土粒子間に生じる摩擦を表わしたものです。これに対し、壁面摩擦角 とは、壁面 ( = コンクリート ) と土の間に生じる摩擦力を表わしたものになります。前項の図にある「物体」を「土」、「傾斜した板」を「コンクリート」に置き換えてみてください。 この値は、擁壁の壁体に土圧が直接作用する時の土圧係数の算定に用いられます。 また下図にあるように、たとえ壁体が鉛直であっても、この摩擦力の存在により、壁体に作用する土圧は壁面摩擦角 δ 分の傾斜をもつことになるので、これを「壁体に対する土圧の作用角」と言い換えることもできるでしょう。 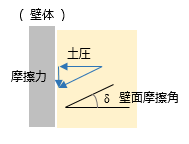 ところで、この値を土質試験によって求めることはできません。 そこでどうしているのかというと、多くの場合、 壁面摩擦角 δ は土の内部摩擦角 φ の 2 / 3 とする というような「経験値」が使われています。クーロン式による土圧係数の算定にあたっては、壁面摩擦角の大小は結果にさほどの影響を与えないので、「大体これくらい」でいいことになっているのでしょう。前述の通り、この値は壁体に対する土圧の作用角ですので、当然ながら、壁体の応力を求める際は作用する土圧の水平成分をとることになります。そこで行政庁によっては、「壁体の応力算定時には土圧の作用角は無視しなさい」としている所もあるようです。これは、上に述べたような壁面摩擦角の値の曖昧さを踏まえた安全側の配慮なのかもしれません。 滑動に対する摩擦係数 擁壁の設計に使用する「摩擦」にはもう一つ、擁壁全体の滑動の検証を行う際に使用する「底版下面と支持地盤の間の摩擦係数」もあります。この場合は「内部摩擦角」ではなく「摩擦係数」の値が直接使われますが、前述の通り、支持地盤の内部摩擦角を φ、摩擦係数を μ とすれば、 μ = tan φ により求めることができます。内部摩擦角は土質試験でを求めればいいわけですが、ここでも例によって「設計の目安値」が公表されています。以下は道路土工指針の値です。
次は宅造法の値。
最後に余談。 昔から疑問に思っているのですが、擁壁の下にはふつう「捨てコンクリート」というものがあります。だからここで問題にすべきは、「コンクリート躯体と支持地盤の間の摩擦」ではなく「コンクリート躯体と捨てコンクリートの間の摩擦」ではないかと思うのですが、違うでしょうか ? ( その 2 につづく ) ツイート( 文責 : 野家牧雄 ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||