|
強制振動
m (
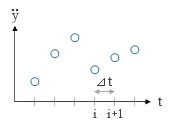
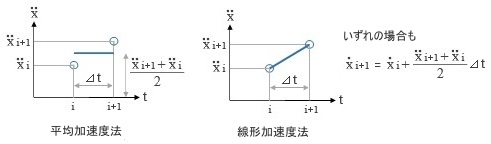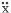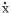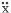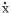その代表的なものが 平均加速度法 と 線形加速度法 です。  上図左にあるのが「平均加速度法」ですが、ここでは、ステップ i と i+1 の間で  は一定になり、その大きさは両ステップの値の「平均」であるとします ( したがって、これを t で積分した  は直線、さらにもう一度積分した x は 2 次曲線になる ) 。一方、ステップ i と i+1 の値を直線で結び、この間で が「線形」に変化すると仮定するのが「線形加速度法」で、これが上図の右です ( は 2 次曲線、x は 3 次曲線になる ) 。ここから先の具体的な数値積分のプロセスについては省略します。興味のある方は他の参考書に当たってください。 先の図に戻りますが、「加速度」を積分した「速度」とは、ここにある青い線分と水平座標軸がつくる四辺形の面積に相当しますので、 i+1 ステップの速度 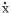は図の一番右に書き入れた式で得られます。で、これをさらに積分したものが i+1 ステップの変位 x になるわけですが、そこにさらに最初に仮定した加速度勾配を加味して式を整理すると ( 例によって結論だけになりますが ) 下のようになります。 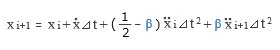 じつは、ここにある係数 β を 1/4 にすると平均加速度法、1/6 にすると線形加速度法になるのです。この考え方を Newmark の β 法 と呼んでいます ( Newmark はこの式の考案者の名前 ) 。 小社で公開中のフリーソフト「かんたん振動解析」に中にも「 Newmark の β 法における β の値」という設定項目がありますが、その意味は以上の通りです。 さて、そうなってくると当然ながら、「一体どちらを使えばいいのか」という話になるでしょう。 いずれの方法も、実際には直線でないものを直線に置換することで近似的な解を求めているわけですが、容易に推測できるように、一般には線形加速度法の方が精度がよいとされます。が、こちらには「解の発散」という問題がある。しばしば「計算不能」に陥ってしまうことがあるのです。 これについては「解析上の時間刻みを小さくする」という対処方法しかありません。多くの地震波データは 1/100 秒の時間刻みになっているので、解析時にこれをさらに細かく分割する ( と言ってもたんに直線補間するだけですが ) 必要が出てきます。そのため、場合によっては 1/1000 秒というような時間刻みを使うことになるのですが、しかし、これはあまり現実的とは思えません。 そういうわけで、一般には平均加速度法を採用することが多いようです。こちらの方が「無難」であることは間違いないでしょう。 |
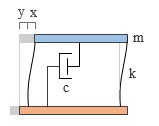
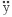が質点に作用しますので、一質点系の振動方程式は以下のようにあらわすことができます ( この場合の x は「相対変位」ということになる ) 。
