|
減衰係数と減衰定数
|
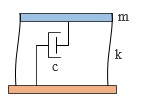
質点系の減衰の機構は、左図にあるような「ダッシュポット」と呼ばれるモデルで描かれることがあります。
これは「圧搾空気が満たされたシリンダー内をピストンが移動する」というイメージですが、ピストンを押す力が速度に比例するのですから、「ピストンを速く押すと抵抗が強く、ゆっくり押すと抵抗が小さい」というわけです。
|
ただし、「減衰の大きさが速度に比例する」というのは物理学的に証明できる事実ではありません。これはあくまでも工学上のモデル化、つまり「減衰という機構は複雑で捉え難いが、とりあえずこういうモデルを作って分かりやすく考えよう」というに過ぎません。
ここまではたんに「減衰」と呼んできましたが、正確な名称は 粘性減衰 です。
この他に、建物の振動エネルギーが基礎を通じて地盤に逸散することによる 地下逸散減衰 があります。さらに、部材の塑性化に伴うエネルギー吸収機構によって生じる 履歴減衰 というのもありますが、これについては後からふれる予定です。
さて、減衰係数 c に速度を掛けたものが減衰という「力」になるのですから、 c の単位は「力 / 速度」です。しかし「力を速度で割る」といわれてもなかなかピンと来ませんね。
そこで一般には、減衰係数 c の替わりに 減衰定数 h という値がよく使われます ( 「係数」「定数」という使い分けもかなり紛らわしいですが ) 。
減衰定数が 1 ( あるいはそれ以上 ) というのは「減衰の力が大きいために揺れない」状態です。
さきほど紹介した「粘性」という用語を使えば、「空気が濃すぎて物体が動かない状態」にたとえられます。この時の減衰係数を 臨界減衰係数 と呼びます。
減衰定数とは、実際の状態がこの臨界状態とどれくらい隔たっているかをあらわす無次元量で、
減衰定数 h = 実際の減衰係数 c / 臨界減衰係数
ということになります ( さきほどの比喩を再び使えば、これは「空気の濃さをあらわす相対的な指数」 ) 。
臨界減衰係数とは、質点が揺れようとする時に、それを「押し返して揺れないようにする」力の大きさですから、質量 m が大きいほど、そしてバネ定数 k が大きいほど大きくなるはずです。具体的にどのような値をとるのかは前項の振動方程式から得られますが、結論だけをいうと下のようになります。
臨界減衰係数 = 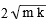
減衰定数 h は、通常、数%程度の値が使われます。日本建築学会「建築物荷重指針・同解説」によれば
コンクリート系の建物で 0.02 から 0.04 くらい
鉄骨系の建物で 0.01 から 0.03 くらい
とされていますが、実際によく使われるのは前者で 0.03、後者で 0.02 というような値です。コンクリート系の方が減衰が大きいのは、材料の組成のルーズさ、あるいは亀裂の発生による揺れの吸収などによるものでしょう。
これに対し、「その 1」で紹介した「設計用の標準応答スペクトル」のようなものは、ほぼ例外なく、減衰定数を 0.05 として作られています。
この値は一般的にいえば大き過ぎますが、ここまで述べてきたような粘性減衰だけでなく、部材の一部の塑性化による履歴減衰などの影響も含めて大き目に値をとったものと考えられます。ただし本当のところはよく分かりません。「長年の習慣」なのでしょう。
減衰定数という値はそれなりの実験あるいは実測に基づいて決められてはいるものの、冒頭にも述べたように、値の性格上、どうしても「大体これくらい」にならざるをえない。しかしその一方、この値の大小が計算結果に与える影響度は、質量や剛性という要因と比較すれば明らかに小さいものです。そんなわけで「大体これくらい」が許容されている、というのが現状なのでしょう。
小社で公開しているフリーソフト「かんたん振動解析」の中に、減衰の設定として「質量比例型」「剛性比例型」「レーリー減衰」という選択肢があります。最後に、このあたりを簡単に説明しておきましょう。
固有円振動数 ω は 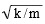 ですが、これを使って先の臨界減衰係数の計算式を書き直すと下のようになります。 ですが、これを使って先の臨界減衰係数の計算式を書き直すと下のようになります。
臨界減衰係数 = 2mω または 2k / ω
ここから、多質点系の減衰量は各次の固有円振動数 ( = 固有周期 ) に依存し、各次数ごとに求める必要があることが分かります。しかし計算の簡便化のため、これを 1 次の固有円振動数で代表させることにしたのが「質量比例型」あるいは「剛性比例型」です。
実際の振動解析では、データとして与えられた減衰定数 h の値を減衰係数 c に変換して使用するわけですが、上の式を使うと、この値は下のように求めることができます。
c = 2hmω または 2hk / ω
ここにある最初の式が減衰係数を質量 m に比例させる「質量比例型」で、二番目の式が剛性 k に比例させる「剛性比例型」です。
( なお、これが意味を持ってくるは多質点系の場合だけで、一質点系では「質量比例」も「剛性比例」も同じになりますが、多質点系については次回から取り上げていきます。 )
もう一つの「レーリー減衰」とは「質量比例」と「剛性比例」を組み合わせたものですが、こちらの説明は省略します。
最も一般的に使われるのは「剛性比例」という考え方です。低中層の建物の場合はこれでとくに問題はありません。
前へ | 1 | 2 | 3 | 4 | 5 | 次へ
|