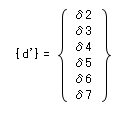15. 部材の内力の計算
部材の内力の計算 |
前回までで「全体剛性マトリクスの作成方法」の話は終わりました。 これが終わってしまえば、変位法の実質部分はほとんど終わったようなものです。後はこれの逆マトリクスを作り(もっとも、ここで逆マトリクスが作成できない場合は「構造体不安定」というエラーが出てプログラムが止まってしまうこともありますが)、下式によって節点変位ベクトル { δ } をもとめます。
{ δ } = [ K ] -1 { P }
しかし当然、設計者にとっては、部材設計のための「内力」という情報も必要ですから、この後の話は、「得られた節点変位ベクトルからいかにして部材の内力をもとめるか」になります。(ここで「内力」といっているのは、前に説明したように、正確には「材端力」、さらに正確にいえば「部材座標系で表現された材端力」のことです。)
さて、部材座標系で表現された材端力ベクトル { p } と材端変位ベクトル { d } の関係は下のとおり( [ k ] は部材の剛性マトリクス)で、私たちがほしいのはこの { p } です。
{ p } = [ k ] { d }
さきほどは、上の剛性マトリクス [ k ] をまずもとめ、それを全体座標系にかんするマトリクス [ k’] に変換した上で全体剛性マトリクスに組み込んだのでした。ですから、私たちは [ k ] の中身ならすでに知っています。
残るは材端変位ベクトル { d } ですが、じつは、これも簡単に分かります。なぜなら、これを全体座標系に変換した { d’} というのは「節点変位そのもの」で、その値はすでに得られているのですから、さきほどとは逆に、この { d’} を今度は部材座標系に変換してしまえばいいのです。その変換式は、
{ d } = [ H ] T { d’}
です( [ H ] は座標変換マトリクス)。
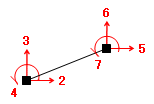
この手順を、さきほどの例題の部材番号 2 (右上がりの梁)について具体的に見てみましょう。
この部材の全体座標系にかんする材端変位と節点自由度の未知数番号の対応は下のようなものでした。
ここで、 11 個の自由度の変位量( δ1, δ2, ・・・ , δ11 )はすでに分かっているのですから、この部材に関係するものだけを拾い出してきてベクトル表示すれば、それがこの部材の { d’}、つまり「全体座標系にかんする材端変位ベクトル」になるはずです。具体的に書けば下のとおりです。
この後はいうまでもありません。座標変換マトリクスを使ってこれを部材座標系にかんする材端変位 { d } に変換し、剛性マトリクスにこれを掛ければ材端力 { p } が得られるのです。注)
注)
すでにお気づきかもしれませんが、これには別の方法もあります。
ここでは、全体座標系の { d’} を部材座標系に変換して { d } を作りましたが、全体座標系に変換された部材剛性マトリクス [ k’] というものも私たちはすでに知ってますから、これを使えば、 { p’} = [ k’] { d’} により、全体座標系にかんする材端力 { p’} を得ることができます。そして、その後でこれを部材座標系にかんする { p } に変換するのです。
もちろん、どちらの方法を使っても答えは同じです。
見てきたとおり、このプロセスはいたって単純です。どういうことかというと、私たちは最初、下のようなプロセスをたどって「節点変位」という解にたどりつきました。
部材座標系にかんする部材の剛性マトリクス [ k ] を作る
▼
それを全体座標系にかんする剛性マトリクス [ k’] に変換する
▼
その [ k’] をもとに全体剛性マトリクス [ K ] を作る
▼
全体剛性マトリクスの逆マトリクス [ K ] -1 を得る
▼
{ δ } = [ K ] -1 { P } により節点変位を得る
で、その「節点変位」が分かったならば、今度は以下のようなプロセスをたどるのです。
{ δ } から部材の材端変位 { d’} を得る
▼
{ d’} を部材座標系に変換して { d } を得る。
▼
{ p } = [ k ] { d } により部材座標系の材端力を得る
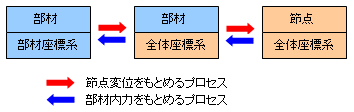
つまり、最初のプロセスは 部材から節点へ、部材座標系から全体座標系へ というものでしたが、今回のプロセスは、節点から部材へ、全体座標系から部材座標系へ というふうに、最初のプロセスを「逆回し」しただけなんですね。
そのあたりを図解するとこんなふうになります。
前に、「変位法の主要なプロセスは節点変位をもとめることにあり、部材の内力をもとめる、というのはその後についてくるオマケみたいなもの」というようなことをいいましたが、その意味が、これで多少理解していただけたのではないかと思います。