前回までで変位法についての基礎的な説明は全部終わりました。
で、これから「基礎編」のあとの「応用編」になるのかというと、別にそういうわけではなくて、もうここで終わりなのですが、最後に、建築物の応力解析でよく使われる「中間荷重の処理」と「壁のモデル化」について説明しておきます。

ここまで述べてきたとおり、変位法における「外力」というのはつねに「節点」に作用するものです。もう少し正確にいえば、「外力は何らかの自由度にかんして作用する」のです。
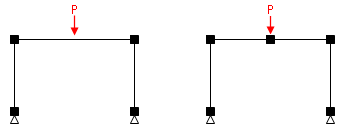
というわけで、下図左にしめすように、もし本来の節点でない場所に外力が作用している（これを中間荷重と呼んだりします）のなら、右にしめすように、その場所にあらたな節点を設ける必要があります。これが、変位法というもののオーソドックスな手続きです。このようにすれば、外力の作用位置の変位や材端力をきちんと計算することができるわけです。

しかし、もしこれが上のような「集中荷重」でなく、長方形や台形の「分布荷重」だったらどうでしょう？
その場合には、要求される精度に応じて部材を何分割かし、各節点に集中荷重を作用させることになりますが、これはこれで面倒な作業です。それに、建築構造材の場合は、たいてい部材中間よりも端部の方が応力が大きくなり、それによって断面寸法が決定されるため、部材中間の変位や応力の分布については「だいたいのところが分かれば困らない」という事情もあります。

そこで、荷重位置にあらたな節点を設けることなく、それを「部材の中間に作用する荷重」としてそのまま扱う、という方法が（少なくとも建築構造計算の分野では）広くもちいられます。
どういう方法かというと、その基本的な考え方は「固定モーメント法」と同じです。固定モーメント法についてはすでにご存知のとおりですが、中間荷重が作用する部材の両端を固定とした時の反力（いわゆる荷重項）をあらかじめもとめておき、それを部材相互の剛性の比におうじて振り分ける、つまり「固定を解除する」というものです。

それと同様に、変位法でも、まず最初に「両端固定とした時の反力」をもとめます。
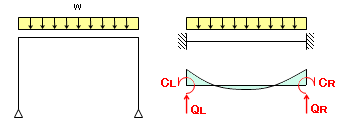
たとえば下図左のような骨組で、梁に作用する中間荷重による両端固定梁の反力モーメントが C 、せん断力が Q であったとします（梁の左右を区別するため、左端に L 、右端に R の添字をつけています。）

ここで、「この骨組内で梁の材端力が両端固定梁と同じになっているような状態」というのを無理やり仮定してみると、下図左にあるような曲げモーメント図が描かれることになります。

しかし、この応力図は明らかにヘンです。「力の釣り合い」を満たしていません。梁の材端力に見合うものがどこにも存在しないからです。
そこで、（梁の材端力についてはすでに分かっているのですから）力の釣り合いを満たすために、図の右にあるように、両端固定梁の反力と同じ「仮想の外力」が部材端に作用しているのだ、と考えることにします。これで、力の釣り合いを満たした立派な「応力図」が出来上がります。

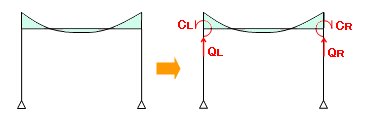
ところで、この外力というのは、あくまでもこちらの都合で勝手に作り上げたもので、実際の骨組にそのような力が作用しているわけではありません。そこでどうするのかというと、これを「解除する」ことにします。「解除する」とは、下図左にあるように、さきほどと逆向きの力 ^注） を骨組に作用させ、これを変位法により解く、ということを意味しています。この結果、下図右にあるような曲げモーメント図が得られます。

注）
これを等価節点荷重と呼びます。この例題では水平の梁を対象にしたため、部材の固定端の反力をたんに逆向きにしたものを作用させていますが、部材座標系と全体座標系が一致しない場合は、もちろん、全体座標系に変換した上で作用させることになります。
また、この例題では部材と直交する方向に荷重が作用しているので、部材の「軸力」は発生しませんが、そうでない場合は、当然、「軸方向の反力」も考慮する必要があります。

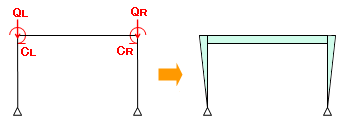
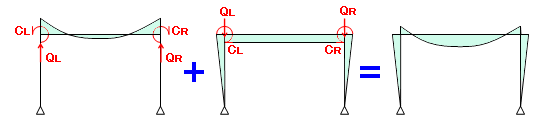
結局、下にしめすように、両端固定梁の応力図と等価節点荷重が作用した時の応力図を足し合わせれば、（両端固定梁の反力が等価節点荷重によって相殺されますので）「等分布荷重が作用している時の曲げモーメン図」が出来上がることになります。^注）

注）
これを重ね合わせの原理と呼びます。つまり、骨組に複数の荷重が作用している時の状態は、それらの荷重が個々に作用している時の状態を重ね合わせたものと同じになる、ということです（ただし部材が弾性範囲内にある場合に限られますが）。
たとえば、「短期の応力とは、長期の応力と地震時の応力を単純に足し合わせたものである」というような考え方がこれに相当します。また、変位法のプログラムでは「部材の中央モーメント」というものを出力してきますが、これは「単純梁とした時の中央モーメント（ M0 ）から両端のモーメントの平均を引いたもの」です。この考え方も「重ね合わせの原理」です。

ただし注意したいのは、この方法で得られるのはあくまでも「部材端」の情報であり、「部材の中間で応力や変位がどのように分布しているのか」についての正しい情報が得られるわけではない、ということです。
たいていのプログラムには「曲げモーメント図」の作図機能がありますが、中間荷重が作用する部材の曲げモーメント図というのは、かならず何らかの「推定」にもとづいて描かれています。
なぜなら、ここまでの話からお分かりのように、部材のどの位置でどのような曲げモーメントになるか、あるいは最大曲げモーメントがどの位置で発生するか、という情報を変位法のプロセスから得ることはできないからです（変位についても同様）。それをちゃんと知りたいのなら、やはり「節点」を設けるしかない、ということになります。
変位法の計算結果の運用にあたり、一応、上のようなことも頭に入れておいた方がよいと思います。

17. 壁のモデル化