14. 全体剛性マトリクス (その3)
全体剛性マトリクスの格納 |
前回述べたような手順で全体剛性マトリクス [ K ] が得られたならば、後は、その逆マトリクス [ K ] -1 をもとめるのみです。そして下式により、もとめていた節点変位ベクトル { δ } が得られることになります。
{ δ } = [ K ] -1 { P }
そういうことではあるのですが、しかしこのコラムは「これから変位法のプログラムを作ろう」という方を対象にしているわけではありませんので、逆マトリクスをもとめるための数値計算の方法についてはふれないことにします(きっと退屈なだけですから)。
前回も、あるいはこれまでもたびたび述べてきたとおり、変位法とコンピュータ処理の親和性は非常に高いのですが、そういうこともあって、「コンピュータプログラムで変位法を扱うための効率的な方法」というものがいろいろと考えられてきました。変位法の理論的な説明をはなれ、今回はそちらの方をながめてみることにします。
この例題での自由度(未知数)の数は 11 でしたので、全体剛性マトリクスの全要素数は 11 × 11 = 121 個です。現在のコンピュータの能力からすれば、この程度の個数のデータを記憶し、その逆マトリクスの演算を行なうのは「何ほどでもないこと」で、それこそアッという間に終わってしまいます。
しかし、これがたとえば 500 節点もあるような骨組だったらどうでしょうか?
この場合、自由度の数を節点数の 3 倍とすれば(支点があるのでこれより若干小さな数になりますが)1500 個ということになり、全体剛性マトリクスの全要素数は 1500 × 1500 = 225 万個です。まあ、場合によっては、それでもやっぱり「何ほどでもないこと」といえるのかもしれませんが、しかし要素数が増えるにつれて「効率の悪さ」というものがどうしても気になってきます。
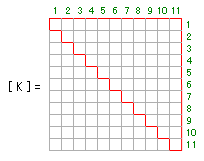
「効率の悪さ」とは何かというと、一つには、すでに述べたとおり、剛性マトリクスは対称なのですから、「片側半分さえ憶えておけば全部憶えたことになるはず」ということです。実際には、下図にあるように、対角要素を含めてその右上(あるいは左下)の三角形部分(赤い線の範囲)さえ記憶しておけばいいのです。これで記憶容量を半分近く節約できます(具体的には、 121 個の要素を 66 個に減らすことができました)。
そしてもう一つは、剛性マトリクスには、
対角線から遠ざかり、外側に近づくほど 0 要素が多くなる
という性質があることです。
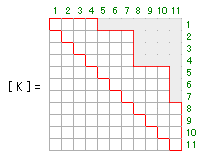
念のため、前回の「最終的な全体剛性マトリクス」を再掲しておきます(グレーの部分が 0 をあらわします)。
これは、(近くにある自由度から順に番号をふっていけば当然そうなるわけですが)「遠くにある自由度ほどたがいに無関係になる」ということをあらわしています。そこで、「ある境界線から外側が全部 0 になることが分かっているのだったら、そこから外側の要素は記憶しないことにすれば記憶容量が節約できる」という考え方が生まれてきます。
先の剛性マトリクスを例にとれば、これは、下図の赤い線の内側だけを記憶する、ということを意味しています(これで、さきほどの 66 個の要素を 44 個まで減らすことができました)。注)
注)
上図にあるような、非 0 要素を取り囲んだ外郭線はスカイラインのように見えなくもないので、このような考え方を「スカイライン法」とよぶことがあります。
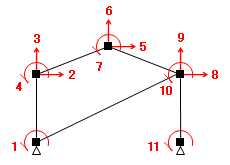
ところで、この例題は一つの節点に最大二つの部材しか取り付かず、しかも「一筆書き」で描けるような骨組に端から順に未知数番号をふっていったものなので、剛性マトリクスの非 0 要素が上図にあるような範囲にきれいにおさまっています。しかし、これではあまりに単純すぎて「きれい事」といわれそうな気もしますので、ここに、下図にあるような「筋かい」を追加してみます。
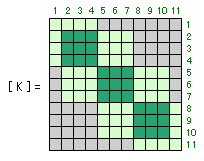
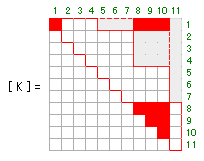
この部材に関連する自由度の未知数番号は何かというと、左下の部材端については 1 だけで、右上の部材端については 8・9・10 の三つです。したがって、この部材の剛性マトリクスを全体剛性マトリクスに組み込むと、下図で赤く塗りつぶした要素があらたに書き換わることになります。
するとどうなるのかというと、「非 0 要素を囲む外郭線」を上図の破線の位置まで拡大しなければいけないことになります。つまり「記憶すべき要素の数」がその分だけ増えてしまうのです(さきほどは 44 個の要素でよかったのが、今度は 59 個に増えていることが分かります)。
ここではもっぱら「自由度の未知数番号」というものを使って説明してきましたが、通常のプログラムでは、ユーザー(データの作成者)が自分でこのような番号をふることはありません。ユーザーが行うのは「節点番号」をふることで、その節点番号の順にプログラム内で「自由度の未知数番号」が自動的に割り振られます。
「変位法のデータを作る場合は、部材両端の節点番号の差ができるだけ小さくなるようにしなさい」というアドバイスをどこかで耳にしたことがあるかもしれません(ないかもしれませんが)。これは何のためなのかというと、まさに今いったようなことで、「節点番号(つまり自由度の未知数番号)の差が小さいほど非 0 要素が一箇所にコンパクトにおさまるようになり、それだけ記憶容量が節約でき、かつ演算が効率的になる」からなのです。注)