13. 全体剛性マトリクス (その2)
全体剛性マトリクスの作成(つづき) |
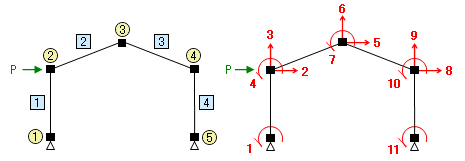
前回の話は、下図左の骨組にたいして下図右のような「自由度の未知数番号」を割り当て、とりあえず、部材番号 1 (左側の柱)の部材剛性を全体剛性マトリクスに組み込む、というところで終わりました。
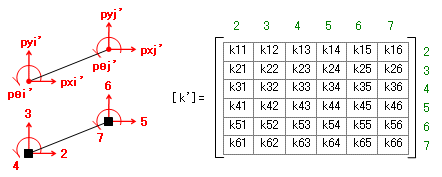
今回の内容はそのつづきですので、つぎは部材番号 2 (右上がりの梁)の番です。この部材の材端力(ないし材端変位)と未知数番号の対応は下図左のようになっており、これをもとに部材剛性マトリクスに未知数番号の「番地」を割り当てると下図右のようになります。
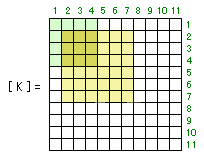
見てのとおり、今回は部材の剛性マトリクスの全要素 6 × 6 = 36 個がなんらかの未知数番号と対応していることになりますから、これを前回と同様にして全体剛性マトリクスに組み込むと下のようになります。
このうち、緑色で塗りつぶした部分は部材番号 1 (左側の柱)の剛性マトリクスから移されたもの、黄色で塗りつぶした部分は今回の部材番号 2 の剛性マトリクスから移されたものをあらわします。また、濃い色で塗りつぶされた部分は両者の値が加算されたことをあらわします。「両者の値が加算された」のはなぜかというと、「未知数番号 2・3・4 については、柱と梁の両方の剛性が関与している」からです。
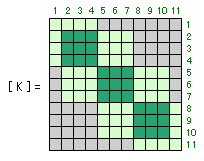
このプロセスを他の部材についても繰返すと、結局、最終的な全体剛性マトリクスは下のようなものになります。
このうち、薄い緑色で塗りつぶした部分は何らかの部材の剛性マトリクスから移されたもの、濃い緑色で塗りつぶされた部分は複数の部材の値が加算されたものをあらわします。
それ以外の、グレーで塗りつぶした部分は、「何の値も入ってこず、最初のままの 0 が入っている」ことになります。「剛性マトリクスの要素が 0 になっている」ということの意味については前にも話しましたが、たとえば上の図で 2 行・ 8 列の値が 0 になっているのは、「 2 番目の自由度(節点 2 の水平方向)の剛性にかんして、8 番目の自由度(節点 4 の水平方向)は直接関与していない」ということをあらわしています。
ここまで見てきたとおり、「部材の剛性マトリクスを全体剛性マトリクスに組み込む」という作業はいたって機械的なものです。なぜそんなに機械的に処理できるのかというと、自由度という未知数に「番地」を割り当てたからです。そして、「番地を割り当てる」という作業がどうして可能になったかというと、いうまでもなく、「マトリクス」を使っているからです。
そしてさらに言うならば、「番地を割り当てる」「番地に値を格納する」「番地を検索して値を取り出す」という作業は、まさにコンピュータのシステムそのものなんですね。「コンピュータによる応力解析とは、ようするにマトリクス変位法のことである」と言われるほどに両者の親和性が高いのは、じつはこんな所に理由があるのです。