12. 全体剛性マトリクス (その1)
例題 |
節点の剛性マトリクスとは「全体座標系であらわされた剛性」であり、同時に「骨組全体の剛性」をパノラマ的にあらわすものです。そこで、これを全体剛性マトリクスと呼んだりします。
今回の内容は、(前回述べた手順で作成した)全体座標系に変換された部材の剛性マトリクスを、どのようにして全体剛性マトリクスに組む込むのか、というものです。
全体剛性マトリクスの作成にはいくつかの方法がありますが、ここでは、もっとも合理的でかつ分かりやすい(と私が思っている)方法を紹介することにします。
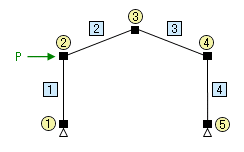
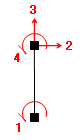
使用する例題は下のような「山形ラーメン」です。
(例によって、節点は塗りつぶした四角形であらわしています。また、丸で囲んだものが「節点番号」、四角で囲んだもが「部材番号」ですが、これらの番号は以後の説明の便宜のためにつけているもので、それ以上の意味はありません。)
さて、まず最初に考えるべきなのは、この骨組にはいったい何個の未知数があるのか、です。この「未知数」とは、もちろん「節点の自由度」のことです。
節点の自由度は一つの節点につき三個(水平・垂直・回転)ありますが、この例題では、節点 1 と 5 は「ピン支点」になっており、水平および垂直方向に固定されています。したがって、これらの節点には回転方向の自由度しか存在しません。
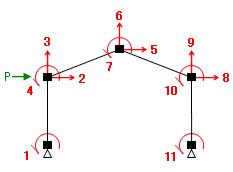
そこで、節点 1 から順に自由度を数えて行き、番号をふったものが下の図です。いってみれば、これは「自由度の未知数番号」のようなものです。
ここから、以下の二つのことが分かります。
1. もとめるべき未知数、つまり自由度の数は全部で 11 個ある。
2. そのうちの 2 番目の自由度(未知数番号 2 )に外力 P が作用している。
ここで、変位法の基本式をもう一度確認しておきましょう。
{ P } = [ K ] { δ }
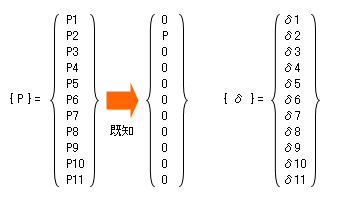
この外力ベクトル { P } と変位ベクトル { δ } の要素数はともに 11 です。これらの各要素に未知数番号の添字をつけてあらわすと下のようになります。
外力ベクトル { P } は「既知」で、ここにあるとおり、 P2 以外の要素は全部 0 になります。変位ベクトル { δ } は、私たちがこれからもとめようとしているものに他なりませんから、もちろん、全体が「未知」です。
ということで、問題は全体剛性マトリクス [ K ] です。
その中身がどうなるのか、今のところ私たちには分かりませんが、しかし「最終的にどのような格好になるか」なら知ってます。「11 × 11 のマトリクスで、その各行・各列が自由度の未知数番号に対応する」のです。
そこで下図にあるように、あらかじめ 11 × 11 のマトリクスを用意し、その要素の値をすべて 0 にしておきます。いってみれば、これは「全体剛性マトリクスの原型」みたいなものです。
後は、必要な場所に数字を入れてこのマトリクスを完成させるのみです。
全体剛性マトリクスの作成 |
部材の断面性能と材料定数、そして部材の長さが分かれば、その部材の「部材座標系にかんする部材剛性マトリクス」が得られる、そしてさらに「部材の傾斜角」が分かれば、それを「全体座標系にかんする部材剛性マトリクス」に変換することができる、というのが前回の内容でした。
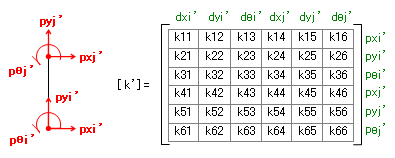
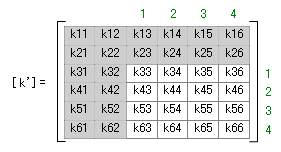
で、そのような手順により、部材番号 1 (左側の柱)の全体座標系にかんする部材剛性マトリクス [ k’] が下のように得られたとします。
これに対し、この柱の材端力(もしくは変位)が骨組全体の未知数番号とどのように関連づけられるかというと、下のようになっています。
これら二つの図を比べてみれば分かるとおり、i 端の pxi’ と pyi’ には対応する未知数番号がありません(支点として拘束されているため)が、その他の材端力(もしくは材端変位)との対応はこんなふうになっています。
pθi’ ( dθi’) → 1
pxj’ ( dxj’) → 2
pyj’ ( dyj’) → 3
pθj’ ( dθj’) → 4
そこで、先の部材剛性マトリクス [ k’] の各行各列に、対応する未知数番号を下のように割り当ててみます。いってみれば、これは自由度の未知数番号によってあらわされた各要素の「番地」のようなものです。
( 1 行目・ 2行目、および 1 列目・ 2 列目は pxi’・ pyi’・ dxi’・ dyi’ にそれぞれ対応するもので、ここでは無関係ですので、グレー表示にしています。)
すでに述べたとおり、剛性マトリクスの m 行・ n 列の要素は「 m 番目の自由度の剛性にかんする n 番目の自由度の関与」をあらわしていますから、たとえば上のマトリクスの 3 行・ 5 列という「番地」にある要素の値 k35 が全体剛性マトリクスの中でどのような意味をもつのかというと、「 1 番目の自由度の剛性にかんする 3 番目の自由度の関与」です。
さて、ここまでくればもうお分かりかと思います。このマトリクス [ k’] は、前項で述べた 11 × 11 の全体剛性マトリクスの「一部分」なんですね。ということは、どうすればいいのかというと、
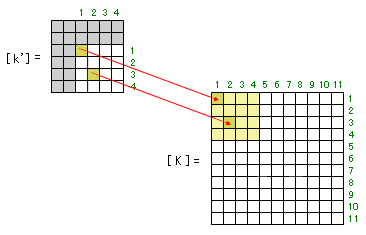
部材剛性マトリクスの各要素の番地に対応するものを全体剛性マトリクスの中に探しあて、その番地に要素の値を足しこんで行けばいい
のです。この様子が下にしめしてあります。
これにより、この部材の剛性マトリクスのうちの有効な値、つまり 4 × 4 = 16 個が全体剛性マトリクスに足しこまれることになります。上図で黄色に塗りつぶした部分がこれに該当します。注)