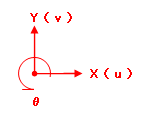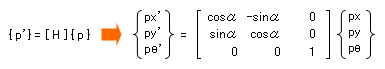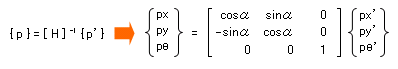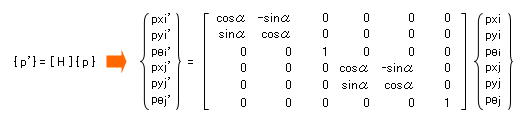11. 座標変換
全体座標系 |
部材の剛性、つまり材端力と材端変位の関係は 6 × 6 の「部材の剛性マトリクス」によってあらわされる、というのが前回の話でした。しかしもちろん、私たちがもとめようとしているのは「節点の変位」であり、そのために必要な「節点の剛性マトリクス」なのですから、「部材の剛性マトリクス」というのは、そこにたどりつくためのプロセスに過ぎません。
節点の自由度にあるとおり、節点に生じる変位(ないしは作用する力)の方向には、水平・垂直・回転の三つがあります。部材座標系と同様、ここでどちらの向きを正方向とするかはその人の自由ですが、一般には下図のような座標系がとられます。これを全体座標系と呼びます。注)
(部材座標系を「x」「y」のような小文字であらわすのに対し、全体座標系は「X」「Y」のような大文字であらわす、という習慣があります。ただし、大文字と小文字の区別というのは何かと紛らわしい部分もあるので、下図の括弧書きにあるような「u」「v」という表記を使うことにもあります。)
注)
部材座標系のところでも説明したとおり、回転の方向については「どちらを正とする」という定まった考え方があるわけではありません。ここでは、部材座標系とあわせるために「反時計回りを正」としています。
座標変換マトリクス |
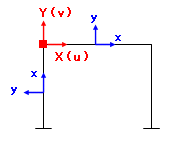
部材の剛性マトリクスから節点の剛性マトリクスを得る、というのは、「部材端の剛性を節点の剛性に変換する」プロセスに他なりません。下の図を見てください。
ここで、左上の節点に着目します。
この節点の水平( X または u )方向の剛性は梁の x 方向の剛性と柱の y 方向の剛性を足したものであり、垂直( Y または v )方向の剛性は梁の y 方向の剛性と柱の x 方向の剛性を足したものです。ここから、
梁については部材座標系の xy を全体座標座標系の XY に置き換えるだけでよいが、柱の剛性を節点の剛性に変換するには、その x 方向を全体座標の Y 方向、 y 方向を全体座標の X 方向に読み替える必要がある
ということが分かります。
しかしもちろん、部材がいつも水平か垂直になっているとは限りません。当然のことながら、「斜め」というのだってあります。
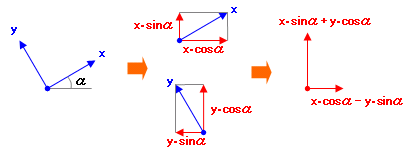
となると、「部材座標系を全体座標系に変換するための一般式」のようなものが必要になってきますが、じつは、これはいたって簡単で、下図のような幾何学的な関係からもとめられます。
結局、部材の傾斜角をαとすると、変換前の部材座標系による材端力 ( px , py , pθ ) を全体座標系に変換したもの ( px’, py’ , pθ’ ) は下のようにあらわされます。
px’ = px・cosα - py・sinα
py’ = px・sinα - py・cosα
pθ’ = pθ 注)
注)
回転方向の力は部材の傾斜角とは無関係ですので、とくに変換する必要はありません。
これをマトリクス形式に書き直すと、座標変換後のベクトル { p’} と座標変換前のベクトル { p } は、下のようなマトリクス [ H ] によって関連づけられることになります。これを座標変換マトリクスと呼びます。
上の式で α を 0 とおくと 「px’= px, py’= py」 になり、これは何も変換しないことと同じです。これが水平部材で、先の図の「梁」に相当します。 α を 90度とおくと 「px’= -py, py’= px」 になり、これは垂直部材、つまり先の図の「柱」に相当します。
ところで、この座標変換マトリクス [ H ] には逆マトリクスが存在します。この逆マトリクス [ H ] -1 は何をあらわすのかというと、先ほどの逆ですから、「全体座標系を部材座標系に変換するマトリクス」ですね。
この逆マトリクスは、なにも面倒くさい計算を行わずとも、先ほどと同様な幾何学的な関係からもとめることができるはずです。結論を言ってしまえば、下のようになります。
ここで、上の [ H ] -1 の中身をよく見てください。これは、じつは元のマトリクス [ H ] の行と列を入れ替えたもの、つまり「転置マトリクス」になっています。ここから、座標変換マトリクス [ H ] には、
その転置マトリクス [ H ] T と逆マトリクス [ H ] -1 がひとしくなる
という性質があることが分かります。この性質は変位法の中でたびたび利用されますので、とりあえず覚えておいてください。注)
注)
ちなみに、このような性質をもつマトリクスのことを「直交マトリクス」と呼びます。
剛性マトリクスの座標変換 |
前項に述べた座標変換マトリクスは、「一つの材端」に関するものですが、ご存知のとおり、部材には i 端・ j 端という二つの材端が存在します。しかし、これらの座標変換はそれぞれ独立して扱うことができますので、二つの材端を同時に座標変換するためには、前項の座標変換マトリクスを拡張した以下のような 6 × 6 のマトリクスを使えばよいことになります。注)
注)
「独立して扱う」というのは、「マトリクス上で関係のない要素を全部 0 にする」ということですから、このマトリクスは、見てのとおり、前項で述べた [ H ] を左上と右下に対角線上に並べ、それ以外の要素を全部 0 にしたものになっています。
材端力ベクトル { p } と材端変位ベクトル { d } の関係をあらわす下の式に戻ります。
{ p } = [ k ] { d }
ここで、全体座標系に変換された材端力ベクトル { p’} と { p } は下の関係にあります。
{ p } = [ H ] -1 { p’} = [ H ] T { p’}
また、これまではもっぱら「材端力」の方について話してきましたが、座標変換の手続きは「材端変位」についても同様ですので、全体座標系に変換された材端変位ベクトルを { d’} とすれば、 { d } との関係は下のようになります。
{ d } = [ H ] T { d’}
これらの関係を最初の基本式 { p } = [ k ] { d } に代入すると
[ H ] T { p’} = [ k ] [ H ] T { d’}
ですが、この両辺に頭から [ H ] をかけると、
[ H ] [ H ] T { p’} = [ H ] [ k ] [ H ] T { d’}
となります。
冒頭の [ H ] [ H ] T は [ H ] [ H ] -1 ということで、その結果は単位マトリクスになります。つまり、この部分は「 1 をかけている」ことと同じですから、結局、
{ p’} = [ H ] [ k ] [ H ] T { d’}
です。
この式をよく見てみると分かりますが、これは、全体座標系に変換された材端力ベクトル { p’} と全体座標系に変換された材端変位ベクトルの { d’} の関係をあらわしたものなのです。
そして、両者の仲立ちをしている [ H ] [ k ] [ H ] T ですが、これはいわば「全体座標系に変換された部材剛性マトリクス」のようなものです。そこで、これを [ k’] であらわすと、
{ p’} = [ k’] { d’} ここに [ k’] = [ H ] [ k ] [ H ] T
ということになります。
で、この後どうするのかというと、もちろん、この [ k’] を節点の剛性マトリクスに組み込むのです。