前回の一番簡単な変位法での例題は、その名のとおりの簡単なものでした。なぜ簡単だったかというと、理由の一つは、節点変位の自由度が実際は三つあるのに一つしか考えなかったことです。
もう一つの理由は、部材の力と変形の関係を「部材の伸び縮み」という一番単純なものに限定したことです。「部材の伸び縮み」をもう少し力学的な表現に直せば「部材の軸方向の変形」ですが、しかし、部材にはこの他に「部材軸に直交する方向の変形」も「回転変形」もあります。

すでにご存知のとおり、部材には「軸力」「せん断力」「曲げモーメント」という三種類の内力がありますが、このうち「軸方向の変形」に対応するのが「軸力」です。ならば同様に「せん断力」と「曲げモーメント」についても変形との対応関係というものがあって、こちらはおそらく、「部材軸に直交する方向の変形」と「回転変形」に関わっているはずです。
しかし結論からいうと、この関係はいささか複雑です。なぜ複雑なのかは、前回の例題がなぜあんなに簡単だったのかを考えてみれば分かります。

前回取り上げた部材の軸方向の変形と内力（軸力）の関係は、他の変形と関係なく独立して存在していました。これに対し、「直交方向の変形」と「回転変形」は独立して存在するわけではなく、つねに「セットになっている」のです。これは、部材の「せん断力」と「曲げモーメント」の間には一定の相関関係があるが、部材の「軸力」はこれらと関係なく独立して存在する、という事実からも裏づけられます。

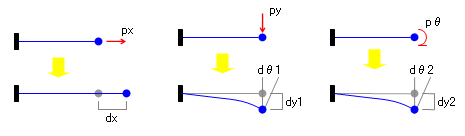
下の図を見てください。（前回は軸力だけを取り上げていたので垂直な「片持ち柱」の図にしていましたが、今回はこれを90度回転させ、なじみのある「片持ち梁」の図に変えています。）

この図の一番左にあるのが「軸力と軸方向変形」ですが、ここにあるとおり、この時にはたんに力の作用方向に変形するだけで、それ以外の変形は起きません。
これに対し、中央にあるのは「片持ち梁先端の力によって軸と直交する方向に変形が生じている」状態ですが、この時には、その方向に変形するだけでなく、同時に「回転変形」も起きていることが分かります。その右にある「片持ち梁先端の曲げによって回転変形が生じている」状態も同様で、回転変形だけでなく「直交方向の変形」も起きています。

というわけで、「直交方向の変形」と「回転変形」についてはセットで考えないといけないのですが、では具体的にどういうセットなのかというと、これまたそう簡単ではありません。もちろん「よく考えれば分かる」ことですが、しかしここではあまり考えているヒマもないので、そこら辺にある「構造力学公式集」を使うことにします。

変位法の基本式 P = K・δ からも分かるとおり、私たちがほしいのは「ある変形を与えた時にどのような力が部材に生じるか」です。残念ながら、公式集にはこういう式はあまり載ってませんが、その逆の「ある力を与えた時にどのような変形が生じるか」ならあります。たとえばこんなふうに。

片持ち梁の先端に垂直方向の荷重 P が作用した時の先端のたわみ量 δ = PL³ / 3EI
同じく、その時の先端の変形角 θ = PL² / 2EI
片持ち梁の先端に曲げモーメント M が作用した時の先端のたわみ量 δ = ML² / 2EI
同じく、その時の先端の変形角 θ = ML / EI
（ L は部材長、I は断面二次モーメント）

剛性と柔性

---

単位の変形を与える力が「剛性」ですが、ここにあるような、その逆の「単位の力によって生じる変形」のことを「柔性」といいます。剛性の逆数が柔性、柔性の逆数が剛性です。

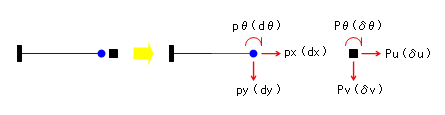
これらの公式にもとづき、さきほどの図にある記号（直交方向の力 py による変形量が dy1 と dθ1、作用する曲げ pθ による変形量が dy2 と dθ2 ）を使い、さらにこれらの合成による最終的な変形量を dy と dθ という記号であらわせば、力と変形の関係は下のようになります。

dy = dy1 + dy2 = py・L³ / 3EI + pθ・L² / 2EI
dθ = dθ1 + dθ2 = py・L² / 2EI + pθ・L / EI

この式は左辺が「変形」になっていますので、下のようにこれらを変形して、左辺を「力」にします。

py = ( 12EI / L³ )・dy - ( 6EI / L² )・dθ
pθ = ( -6EI / L² )・dy + ( 4EI / L )・dθ

部材の軸方向の力と変形については前回述べたとおりですが、ついでに、上と同様の記号を使って下のようにあらわしておきます。

px = ( EA / L )・dx

結局、これら三つの式が部材の力と変形の関係 ^注）、つまり「部材の剛性」をあらわしていることになります。

注）
ここで「力と変形の関係」という時の「力」とは、ここまで見てきたとおり「部材端に作用する力」のことです。では、これは部材の内力（軸力・せん断力・曲げモーメント）のことなのかというと、「そう考えてもらっても構わないが、しかし本当は少し違うもの」です。このあたりのことは、後からくわしく見ていくことにします。

次にやるべきことは、前項でえられた「部材の剛性」を「節点の剛性」に変換することですが、下の図からも分かるとおり、片持ち梁先端の変形方向は節点変位が生じる方向と一致しています。^注）

注）
というよりも、これは「部材の変形方向と一致するように節点変位の方向を決めた」という、それだけのことです。
一般には、ここで「部材端の力（変位）の方向を節点の力（変位）の方向に変換する」という手続きが必要になるのですが、このあたりについては後から取り上げます。

したがって、上図の記号にしたがい、部材の内力をあらわす px・py・pθ をそのまま節点の外力 Pu・Pv・Pθ に、部材の変形をあらわす dx・dy・dθ をそのまま節点変位 δu・δv・δθ に置き換えて前項の式を書き直せば、

Pu = ( EA / L )・δu
Pv = ( 12EI / L³ )・δv - ( 6EI / L² )・δθ
Pθ = ( -6EI / L² )・δv + ( 4EI / L )・δθ

となります。これが変位法の基本式 P = K・δ の「内訳」です。
ここでの未知数は δu・δv・δθ の三つで、方程式が三つありますから、いわゆる「三元連立方程式」としてこれを解くことができます。この後の処理は一番簡単な変位法にあるのとまったく同じで、得られた節点変位を部材の変形量に置き換えた後、前項にある各式にそれを代入すれば部材の内力がもとまる、というわけです。

ここまで述べてきたのが「変位法」といわれるものの基本原理です。
「なんだ、それだけのことか」と思えばたしかにそのとおりで、たとえばここで話題にした片持ち梁のようなものであれば、電卓でも十分に計算できます。しかしもちろん、それは未知数の数（つまり自由度の数）が少ないからで、これがたとえば 100 節点もあるような骨組であれば、自由度の数は 300 に上ることになり、300 元の連立方程式を解かなければなりません。いくらなんでも、これを電卓でやろうとする人はいないはずです。

というわけで、ここに「コンピュータ」の出番がやってきます。これを使えば、何百元の連立方程式だって力まかせに解くことができるからです。
これが、変位法が「コンピュータ向きの応力解析方法」とされ、現在広く使われている理由の一つですが、しかしたんにそれだけではありません。それに加えて、あるいはそれ以上に「変位法のロジックとコンピュータプログラムのロジックの相性の良さ」というものを取り上げないわけにはいきません。そして、その相性を取り持っているのが、じつは「マトリクス」という考え方です。

ここまではもっぱら「変位法」という言い方をしてきましたが、これは別名「剛性マトリクス法」あるいは「マトリクス変位法」ともいわれます。ようするに、変位法とは「マトリクスを使って応力解析を行なう方法である」と定義してもいいようなもので、「マトリクスを知らずに変位法を語るなかれ」なのです。
となると、次の話題は当然、「そのマトリクスとはいったい何なのか？」になります。

5. マトリクスとは？ （その1）