耐力はバラつく
建物の安全性は「耐力」と「荷重効果」の比較によって表される、そして荷重には「不確定性」がある、というのが前項の話でしたが、何も荷重だけが不確定性を持っているわけではありません。そのあたりはの事情は「耐力」の方だって変わりはないでしょう。
前項では 500mm 角のコンクリート柱を例にとり、「その許容耐力は 4000kN だが、本当の耐力は 6000kN である」と言いました。それにしても、これは本当に本当の耐力なんでしょうか?
建設現場では、実際に打設したコンクリートから複数のコアサンプルを抜き取り、それをを潰して強度を確認するという検査がよく行われます。この時、設計基準強度 24N/mm2 のコンクリートから採取されたサンプルのすべての強度が正確に 24.0N/mm2 になる、などということは絶対にありえません。そこには必ず「バラつき」「不確定性」があります。
では、それらの「平均値」が 24N/mm2 になるかというと、そういうわけでもない。たいていの場合、平均値はそれよりも大きくなります。なぜなら、ほとんどの場所で設計基準強度を上回るように、あらかじめ設計基準強度よりも大きな強度(「調合強度」と呼ばれる)を目標としてコンクリートが調合されているからです。
そして、その調合強度を決める際に使用されるのが「確率・統計」の考え方になります。
先に述べたとおり、限界状態設計法は建物の安全性を「確率」に基づいて表現するものです。したがって、これを理解するためには、「確率」あるいは「統計」に関する基礎的な知識がどうしても必要になります。
そこで、確率と統計に関する基礎的な用語を以下でおさらいしておくことにしますが、あらためて断るまでもなく、私は高い所から確率統計論のレクチャーを始めるようなガラではありませんから、以下の話はあくまでも、「一通り知っておく必要があるごく初歩的な知識」の範囲にとどまります。
したがって、そんな話を改めて聞く必要がない方は以下をスキップしてください。
さて、さきほどから話題にしている「コンクリート」を例にとって話しますが、どんな生コン工場でも、どくらいの水とどれくらいのセメントを混ぜればどれくらいの強度のコンクリートが出来上がるか、というデータを持っています。ですから、設計基準強度が 24kN/mm2 になるようなコンクリートを作ってくれ、と言われればそれは簡単にできます。
しかし、そのようなコンクリートを調合し、出来上がったものから複数の供試体をとって潰してみると、その強度には必ず「バラつき」が出る。
そこで、計測された強度を、たとえば「 0 から 1kN/mm2 の範囲」「 1 から 2kN/mm2 の範囲」というふうにグループ分けし、それぞれのグループに分類される供試体の数を集計して棒グラフに表すことを考えてみます。
そのグラフが結果的にどのようなものになるか、ということは容易に想像できるでしょう。
なにしろこのコンクリートは、過去の実績に基づいて強度が 24 になるように調合されていたわけですから、当然ながら、その値が 24 前後になる所の棒グラフが最も高くなり、そこから(小さい側あるいは大きい側に)外れるほど棒グラフが低くなるはずです。
そしてさらにもう一つ、「すべてのデータを平均すれば、その値はほぼ 24 になるであろう」ということも推測できます。
もちろん、供試体の数が少なければ全体はデコボコな形のグラフになりますが、(あくまでも理論上の仮定として)すべての場所から供試体を採取してそのデータを集計し、棒グラフの頂点をつないで行くと、それは下図に示すような「平均値をはさんで両側に裾野が左右対称に広がっている」ような形になると考えられます。
この時、このデータの一群は「正規分布している」と言います。
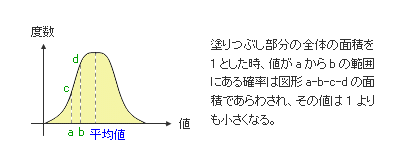
上図において、正規分布曲線の内側の面積(塗りつぶし部分)は検査対象としているコンクリートの全ボリュームに相当しますが、これを 1 という指数であらわすことにします。注)
注)
実際には、あらゆる場所から供試体を抜き取ることは不可能です。しかし、検査対象となっているものの全体(これを統計用語で母集団という)のボリュームに対して一定数以上の供試体(これを統計用語で標本という)を採取して集計すれば、元の母集団の性状を近似できることが分かっています。
ようするに、これが「統計」という考え方です。
身近な例として「テレビの視聴率調査」「世論調査」のようなものをあげることができます。この時の母集団は「その時間帯にテレビを見ている人の総数」あるいは「その時点における日本の総人口」になりますが、それが分からなくても、一定数以上の標本を偏りなく採取すれば全体の性状をよい精度で推測できるのです。
ここで上図にあるように、任意に取り出したサンプルの値が a から b の範囲内にある可能性を考えてみます。
この条件に含まれるデータの全体は図形 a-b-c-d の面積に相当し、それを指数で表わしたものは必ず 1 よりも小さくなるはずですが、この面積(これを確率密度という)を P という記号で表わした時、
あるデータが a から b の範囲の値をもつ確率は P である ( 0 < P ≦ 1 )
と言います。
正規分布の曲線がどのような形状をとるのかは一つの数式で簡潔に表わされていますが、それに関与するパラメータは、ここまで述べてきた「平均値」だけではありません。曲線の「山」あるいは「裾野」の形状がどのようになっているか(切り立っている・緩やか等)という情報が必要です。
つまり、「おのおのの値が平均値の周辺にどのようにバラついているか」を知らなければなりません。
これを表わすのが分散という値で、以下の式で表わされます(Σは全データについての集計を表わす)。
分散 = Σ( 各データの値 - 平均値 ) 2 / ( データの総数 )
この値の分子が「各データの値 - 平均値」でなく、その 2 乗になっているのは、おのおのの値が平均値に対してプラス側とマイナス側に均等に分布しているため、たんに「各データの値 - 平均値」を集計すると、その合計値が必ず 0 になってしまうからで、つまり 2 乗することによって「プラス側」「マイナス側」の差異を消しているのです。
結局、この値が大きいほど「各データの値がバラついている」「山が緩やかで裾野が大きい」ということになりますが、ただし上記の通り、この値は実際の値の 2 乗になっているため、元のデータと単位が合いません。
そこで、この値の平方根をとって元のデータと単位を合わせたものを作ることにしました。これが標準偏差です。
標準偏差 = √ ( 分散 )
この値の持つ意味は「分散」と同じですが、これは原データと同じ単位を持っているため、確率分布の曲線上にプロットすることができます。
下図にあるように、平均値を中心としてその両側に標準偏差の幅を持つ線を引くと、結果的に、この幅の間には総数の約 68% に相当するデータが含まれることが数学的に証明されています。
つまり、「平均値 ± 標準偏差」の範囲の値を持つデータは全体の約 7 割を占めているので、もしそのような値が検出されたら、それは「ごくふつうのデータである」と考えていいのです。
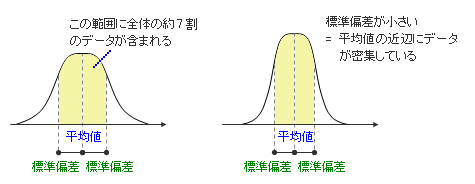
これが確率分布曲線の形状にどのように表れるかということをもう一度確認しておきますが、標準偏差が大きいということは、全体の約 7 割のデータがそれだけ大きな範囲の中に散らばっているわけですから、データのバラつきが多く、曲線の勾配が「緩やか」になります。これに対し、標準偏差が小さいということは、平均値に近い値が狭い範囲に密集しているということですから、その分だけ勾配は「急」になるのです。
ここからの話で分かるように、あるデータの値が母集団の中でどのような性格(「ふつう」なのか「特異」なのか)を持つのかを、たんに平均値との差だけから推測することはできません。そこで、
( データの値 - 平均値 ) / 標準偏差
という値を使って評価することがよく行われます。
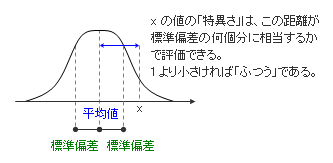
これは、そのデータと平均値の差が標準偏差の「何個分」に相当するかを表わしています。この値が 1 より小さければ、それは標準偏差内におさまる「ふつうの値」になり、1 より大きくなればなるほど「特異な値」であることが分かるのです。注)
注)
ついでに余計な話をしておきますと、試験の点数の「偏差値」はこのような考え方に基づいて作られたものです。
たとえば平均点 50 点に対してあなたの点数が 65 点だったという場合、その点数の価値は、たんに平均点との差だけでは分かりません。そこで、その点数の平均値との差(この場合は 65 - 50 = 15 )を標準偏差で割り、この値が大きい人ほど高い偏差値を与えるような仕組みになっています。
ここから再びコンクリートの話に戻ります。
生コン業者が設計基準強度 24 のコンクリートを受注した場合、正しくその強度を目標にしてコンクリートを調合したらどうなるでしょうか?
当然、その強度の「平均値」が 24 になります。そして正規分布の原則に従えば、全体のの半分は設計基準強度を下回っているはずです。つまり、不良率(実際の強度が目標値を下回る確率)が 50% になります。
これではいかにも困るでしょう。しかし、かと言って、不良率を限りなく 0 に近いものにしようとすると、強度 24 のコンクリートを作るために、強度がその倍以上も出るようなコンクリートを調合しなければならなくなります。これはいかにも不経済で、昨今ならばたちまち「地球資源の浪費」と言われかねません。
そこで一般にとられるのが、「不良率を 5% 程度にする」という考え方です。
「 95% の確率で設計基準強度を上回っているのであれば、残りの 5% には目をつぶる」ことにするのです。
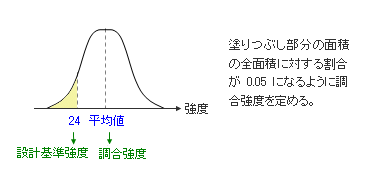
つまり下図に示すように、強度が 24 以下になる範囲の確率を 0.05 とし、そこから正規分布の曲線に基づいて「平均値」を逆算します。これが「調合強度」と呼ばれるものです。当然ながら、標準偏差の小さなコンクリートを作れる工場ほど調合強度を小さくすることができることになります。
それからもう一つ、変動係数という値があります。
さきほど、「標準偏差の小さなコンクリートを作れる工場」と言いましたが、一般に、強度の大きなコンクリートを作ろうとすればするほど正規分布曲線の「横幅」が大きくなりますから、それに伴って標準偏差の値も大きくなると考えられます。したがって、その工場の能力をたんに標準偏差だけで表わすことはできません。
そこで、標準偏差を平均値で割った無次元数を考えることにしたのですが、これが「変動係数」です。つまり、
変動係数 = 標準偏差 / 平均値
で、この値が小さいほど正規分布曲線の勾配が「急」で平均値の近辺に値が密集していることになります。
この値は工学上でしばしば使われますので、覚えておいて損はないでしょう。
別に、私はここで「コンクリートの調合強度の決め方」の話をしようとしたわけではありません。「耐力というものにはバラつきがあり、確率的にしか定めることが出来ない」ということの一例として「コンクリート強度のバラつき」という話題を取り上げたのでした。
−−限界状態設計法の話に戻ります。
