9. 部材の力と変形 (その1)
ここまでの復習 |
ここまでの話は、「変位法とはおおよそこんなものである」という内容で、変位法の輪郭をとらえることを目的とした、いわば「総論」でした。ここから先が「各論」になりますが、その前に、これまでの内容をもう一度復習しておきます。
1.
変位法とは節点変位をもとめる方法である。
2.
節点変位 { δ } は、その剛性 [ K ] と外力 { P } の関係であらわされる。これが変位法の基本式 { P } = [ K ] { δ } である。
3.
節点の剛性は何によって決まるのかというと、それは「部材の力と変形の関係」である。これをもとに剛性マトリクス [ K ] が得られる。
4.
剛性マトリクス [ K ] が得られれば、(不安定構造でないかぎり)その逆マトリクス [ K ] -1 がもとまる。
5.
その結果、{ δ } = [ K ] -1 { P } により節点変位がもとまる。
6.
節点変位が分かれば部材の内力がもとまる。
部材座標系 |
最初は、節点の剛性マトリクス作成の基礎となる「部材の力と変形の関係」の話です。
ここにいう「部材」とは、「直線をなしていて、かつ全長にわたってその断面性能が均一なもの」ですが、であるからには、部材にはかならず「始め」と「終わり」があることになります。それをどのように呼ぶかは人の好き好きですが、一般には「始端・終端」「1端・2端」「i端・j端」のような呼ばれ方をします。注)
ここでは「i端・j端」を使うことにします。
注)
もちろん、これは二つの部位をたんに識別するためのもので、どちら側を「始まり」にするかは、その人(設計者ないしはプログラムのデータ作成者)の勝手です。片方を「始まり」と決めたらもう一方は「終わり」になる、というただそれだけのことに過ぎません。
部材端の力ないし変位には以下の三つの方向があります。
部材の軸方向に沿ったもの ( → 軸力 )
部材の軸方向に直交するもの ( → せん断力 )
回転 ( → 曲げモーメント )
ご存知のとおり、部材の内力には「軸力」「せん断力」「曲げモーメント」の三種類がありますが、上の括弧内にしめしたとおり、この三つの方向は、これらの内力にそれぞれ対応するものです。
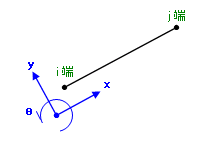
さて、これらの力と変位の関係をさだめるにあたり、まず必要なのはそれらの「向き」、ようするに「どちらが正方向なのか」を決めておくことです。これは 部材座標系 と呼ばれます。
もっとも一般的な部材座標系の決め方は、
部材の i 端から j 端に向かうものを 部材x軸 とし、それを反時計回りに 90 度回転させたものを 部材y軸 とする
というものです(部材座標系については、x あるいは y のように小文字で表記する習慣があるので、ここでもそれにしたがっています)。
図示すれば下のようになります。
部材座標軸をどのようにとるか、つまり「どちらを正方向にするか」というのはたんなる「決め事」で、どのようにするのが正しい、という性格のものではありません。どう決めようとも、それで一貫しているのであればそれはそれでいいのですが、上にしめしたような x軸・ y軸のとり方というのは、どんなプログラムでもほぼ例外なくこのようになっているはずです。
しかし、次の「回転」については必ずしも決まった考え方があるとはいえません。これは平たくいえば「時計回りを正とするか、反時計回りを正とするか」という問題ですが、一つの考え方は、数学的な表現で角度を扱う場合は「反時計回りが正」なのでそれにしたがう、という立場です(ここではこちらを採用しています)。
一方、時計回り・反時計回りという言い方にあらわれているとおり、私たちには時計回りを「順回り」、反時計回りを「逆回り」というふうに考える習慣があります。これにしたがえば「時計回りが正」という考え方にも理があることになります。まあしかし、さきほども言ったように、これはたんなる「決め事」で、「どちらが正しい」というような問題ではありません。
材端力と内力 |
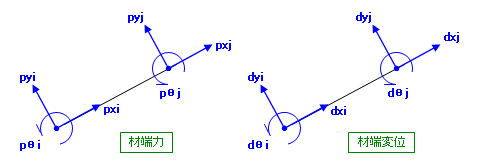
部材の力と変形の関係は、部材端の力と変位の関係としてあらわされます。以後、前者を材端力、後者を材端変位と呼ぶことにします。
この「材端力」は、これまでさんざん述べてきた「(節点に作用する)外力」とは違います。では「内力」なのかというと、(後から述べるように)それと密接な関係にはありますが、しかし内力そのものではありません。
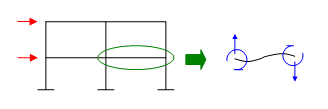
下図のような骨組に外力(赤い矢印)が作用すると、その影響で、各部材になんらかの「変形」が生じます。当然、「変形」が生じれば「内力」も発生します。
ここで、上図右にあるように、変形を受けている任意の一部材を取り出してみると、この部材に作用する直接的な外力は何もないことが分かります。しかし、にもかかわらず、部材はたしかに「変形」しているのですから、この両端には なんらかの力(青い矢印)が作用しているのだ、と考えられます。この なんらかの力 が「材端力」です。
この力は、もちろん、節点に作用する外力を原因として生まれますが、同時に、部材の変形や内力の原因にもなります。そういう意味では、「材端力とは、節点に作用する外力と部材に発生する内力の仲立ちをするものである」というふうに考えることもできそうです。
さて、部材端には i 端・j 端の二つがあり、力(変位)には三つの方向があるのですから、下図にしめすように、ここには計 6 個の力(変位)が存在していることになります。部材の力と変形の関係とは、結局、この 6 個の材端力と 6 個の材端変位の関係である、ということです。
これらの材端力の間には、力の釣り合いにより、以下の関係があります。
pxi + pxj = 0 つまり pxi = - pxj
pyi + pyj = 0 つまり pyi = - pyj
ここで、 pxi ならびに pxj という力は部材の「軸力」に対応し、pyi ならびに pyj という力は部材の「せん断力」に対応するものですから、これらの式から、「部材の軸力とせん断力の大きさはつねに一定である」ということが分かります。注)
注)
変位法の特殊なケースとして、「部材の中間に作用する荷重」というものを考えることがありますが、その場合にはこの関係は当てはまりません。ここでの話は、変位法の基本にしたがい、「すべての外力は節点に作用する」とした場合のものです。
「部材の中間に作用する荷重」の取り扱いについては後から取り上げることにします。
いま、「・・・ということが分かる」などと言ってしまいましたが、しかしよくよく考えてみると、これは軸力なりせん断力なりの定義そのものである、と言ってもいいわけです。どういうことかというと、
軸方向の材端力が一端で N、他端で -N になっているような状態の時、「この部材には N にひとしい大きさの軸力が発生している」という
のであり、同様に
軸の直交方向の材端力が一端で Q、他端で -Q になっているような状態の時、「この部材には Q にひとしい大きさのせん断力が発生している」という
のですが、さらに下のようなことも言えます。
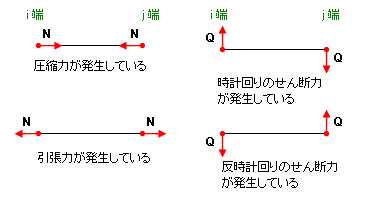
軸方向の材端力が「i 端で正・j 端で負」ならば、その部材の軸力は「圧縮」で、その逆の場合は「引張り」である。
軸に直交する方向の材端力が「i 端で正・j 端で負」ならば、その部材のせん断力の向きは「時計回り」で、その逆の場合は「反時計回り」である。
この軸力・せん断力とは、もちろん部材の「内力」ですが、ここまでの話から明らかなように、部材の「内力」と「材端力」は同じものではありません。
にもかかわらず、応力計算プログラムで「部材の応力」なるものを出してみると、「i 端側の軸力が 10kN、j 端側の軸力が -10kN」のように書かれていたりします。これは何なのかというと、正確には部材の「応力」(私たちの言い方を使えば「内力」)ではなく、「材端力」のことなんですね。注)
ですから私たちとしては、もし上のように出力されてきたら、「この部材には 10kN の圧縮力が発生しているのだな」と「翻訳」する必要がある、ということになります。
注)
これは前にも言いましたが、「応力」の厳密な定義は「単位面積あたりの力(いわゆる応力度)」です。しかし現在、「応力」という言葉はかなり広義かつアイマイに使われていますので、「なんらかの外力の影響により部材に生じる力の総称を応力という」のだとすれば、ここでいう「材端力」のことを「応力」といっても、それはそれで間違いではない、ということになるのでしょう(たぶん)。
さて、残るは「回転方向の力」ですが、これは部材の「曲げモーメント」に関連づけられます。
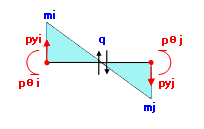
軸力・せん断力が一定になるのに対し、曲げモーメントは「一定に変化」します。つまり、直線的に変化します。この様子を下に「曲げモーメント図」としてしめしておきます。注)
注)
このコラムをご覧になっている方にこんな説明をするのは「釈迦に説法」かもしれませんが、念のために言っておきますと、上の図で、材端の回転力の向きが両端とも同じになのに、どうして曲げモーメント図の描き方が上下に反転しているのかというと、「曲げモーメント図は部材に引張側の応力度が生じるような方向に描く」というルールがあるからです。
この時、部材 i 端の曲げモーメント mi の大きさは材端力 pθi にひとしく、 j 端の曲げモーメント mj の大きさは材端力 pθj にひとしくなります。さらに、部材のせん断力 q の大きさは材端力 pyi または pyj にひとしくなりますが、周知の通り、「せん断力の大きさは曲げモーメントの変化率(勾配)にひとしい」のですから、これらの間には以下のような関係が成り立っているはずです( L は部材の長さ)。
( pθi + pθj ) / L = pyi または ( pθi + pθj ) / L = -pyj
これを変形すると下のようになります。
pθi + pθj - L・pyi = 0 または pθi + pθj + L・pyj = 0
この式は何なのかというと、じつは、最初の式が j 端回りのモーメントの釣り合い、二番目の式が i 端回りのモーメントの釣り合いをあらわしているだけです。