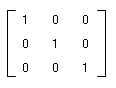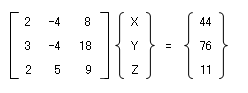6. マトリクスとは? (その2)
マトリクスとマトリクスの掛け算 |
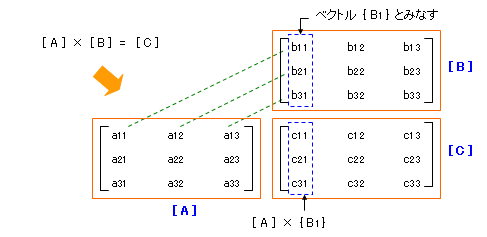
つぎはマトリクスどうしの掛け算ですが、これはマトリクスとベクトルの掛け算の応用と考えることができます。下に、[ A ] × [ B ] = [ C ] のようすをあらわしておきます。
まず、[ B ] の 1 列目をベクトル { B1 } とみなし、前回の要領で [ A ] × { B1 } の計算を行います。するとその結果、 { B1 } と同じ要素数をもつベクトル { C1 } がえられます。これが最終的にもとまるマトリクス [ C ] の 1 列目の値です。以下、 2 列目以降についても同様の手順を繰り返せば [ C ] の全体がもとまる、というわけです。
このことから、マトリクスとマトリクスの掛け算には以下のようなルールがあることが分かります。
[ A ] × [ B ] = [ C ] の掛け算を行う場合、先のマトリクス( A )の列数と後のマトリクス( B )の行数は同じでなければならない。
また、掛け算の結果として得られるマトリクス( C )の行数は先のマトリクス( A )の行数と同じになり、列数は後のマトリクス( B )の列数と同じになる。
さらに、以下のようなことも分かります。
[ A ] × [ B ] と [ B ] × [ A ] は、一般に、同じにはならない
しかし、ここで話したことはあまり重要ではありません。
なぜなら、マトリクスの掛け算というのはコンピュータプログラムがやってくれるもので、自分で電卓を叩いて計算したりはしないからです。マトリクスどうしの掛け算のやり方というのは、「知らないよりは知っておいた方がいいが、忘れてしまっても大して困らない」という程度のものです。
ただし、以下のことはぜひ憶えておいてください。
実数 A (ただし 0 以外)にその逆数 1 / A (またはA -1 )が存在するように、マトリクス [ A ] にもその逆数 [ A ] -1 が存在するならば、これを逆マトリクスという。
逆マトリクス |
元の数 A にある数 B を掛けた答えが 1 になるような時、 つまり A × B = 1 の関係にある時、B は A の逆数である、といいます。
同様に、元のマトリクス [ A ] にあるマトリクス [ B ] を掛けた答えが [ 1 ] になるような時、 つまり [ A ] × [ B ] = [ 1 ] の関係にある時、[ B ] は [ A ] の逆マトリクスである、といいます。
では、この [ 1 ] とはなんなのかというと、下図にあるような「対角線上にある要素が 1、それ以外の要素が全部 0 になっているような正方マトリクス」で、これを単位マトリクスと呼びます。
(もっとも、 [ 1 ] などというマトリクスの表記はありません。通常、単位マトリクスには [ I ] あるいは [ E ] のような表記が当てられます。以後は [ I ] と呼ぶことにします。)
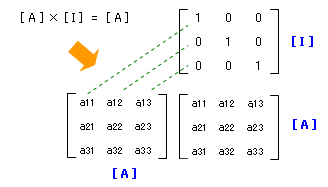
実数の 1 とは「それに何を掛けてもその答えが掛けたものと同じになるような数」ですが、それと同様に、単位マトリクスとは「それに何を掛けてもその答えが掛けたものと同じになるようなマトリクス」です。
上にあるのは 3 行 3 列の単位マトリクスですが、同様な 3 行 3 列のマトリクス [ A ] との掛け算の様子を先ほどと同様のやり方であらわすと下のようになります。
つまり、
[ A ] × [ I ] = [ A ] ということは [ A ] × [ A ] -1 = [ I ]
です。
しかし、ことはそれほど単純ではありません。どんなマトリクスにもその逆マトリクスが存在するのかというと、そういうわけではなく、「逆マトリクスが存在するための条件」というものがちゃんとあるからなんです。
逆マトリクスが存在するための条件 |
前回述べたように、変位法の基本式は { P } = [ K ]・{ δ } で、先の片持ち梁の例についていえば、これは以下の三つの式をまとめてあらわしたものです。
Pu = ( EA / L )・δu
Pv = ( 12EI / L3 )・δv - ( 6EI / L2 )・δθ
Pθ = ( -6EI / L2 )・δv + ( 4EI / L )・δθ
ここで私たちがもとめようとしているもの、つまり「未知数」は δu・δv・δθ の三つです。ということは、これはようするに「三元連立方程式」で、この方程式を解けば三つの未知数がもとまる、ということなのです。
これを、いま学んだばかりの「逆マトリクス」の知識を使って言い換えてみます。
変位法の基本式は { P } = [ K ] ・ { δ } で、未知数は { δ } である。
この式を変換すると { δ } = [ K ] -1・ { P } になる。
ということは、逆マトリクス [ K ] -1 が分かれば未知数 { δ } がもとまるはずである。
つまり、先の三元連立方程式を解くことと逆マトリクス [ K ] -1 をもとめることは、「同じことの言い換え」なんですね。
連立方程式の解き方なら、むかし中学校で習いました。
それでは下の問題を解いてみてください。(いや、べつに本当にやらなくても結構ですが、答えを先にいってしまうと、「 X = 2, Y = -4, Z = 3 」です。)
2X - 4Y + 8Z = 44
3X - 4Y + 18Z = 76
2X + 5Y + 9Z = 11
上の式を「ベクトルとマトリクスの積」としておらわすと下のようになります。
連立方程式を解くとき、私たちはまず、これを変形することによって未知数の数を減らしてゆき、最終的に一つの未知数だけを含む式にしてこれを解きます。あとは、得られた未知数の値を順次代入していけば他の未知数の値が得られます。
これ以上くわしい説明はしませんが、これはガウスの消去法と呼ばれる解法で、じつは、逆マトリクスをもとめる場合もまったく同じようなことをしているのです(興味のある方は他の本なり関連のウェブサイトなりを参照してください)。
とりあえず私たちにとって重要なのは、「どのようにして逆マトリクスをもとめるか」ではなく、「逆マトリクスが存在するための条件とはなんなのか」です。
逆マトリクスをもとめることは連立方程式を解くことと同じである、といいました。であるのならば、「逆マトリクスが存在しない」は「連立方程式に解が存在しない」と同じはずです。
連立方程式に解が存在する最初の条件は「未知数の数と方程式の数が同じであること」です(むかし学校でそのように習いました)。ですから、下のような連立方程式は解くことができません。
2X - 4Y + 8Z = 44
3X - 4Y + 18Z = 76
ここで、連立方程式をマトリクス表示にした先ほどの図をもう一度見ていただきたいのですが、方程式の数というのはマトリクスの「行数」のことです。そして、未知数の数というのはマトリクスの「列数」のことです。
ということは、
そのマトリクスに逆マトリクスが存在するためには、それが行数と列数が等しい「正方マトリクス」である必要がある
のです。
幸いなことに、剛性マトリクスは「自由度の数を行数および列数とする正方マトリクス」ですので、この条件は満たしています。
しかし、正方マトリクスならなんでもいいわけではなく、その「中身」も大いに関係してきます。たとえば下のように、マトリクスのある行の値が全部 0 になっていたとしたらどうでしょう?
この場合、3 行目は「何もない」のと同じですから、見かけは 3 行 3 列の正方マトリクスでも、実質的には 2 行 3 列のマトリクスだといえます。つまりこれは「方程式の数が一つ減った」ことと同じなので、このマトリクスの逆マトリクスは存在しません。
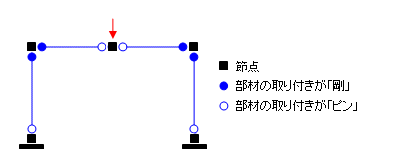
では具体的にどういうケースでこういうことが起きるのかというと、たとえば はじめに で取り上げた「四ピンラーメン」のような場合です。節点の自由度 で再びこの骨組を取り上げ、下のように図解して説明しました。
その中で、「真ん中の節点(赤い矢印)の回転方向の自由度に関する剛性がないのでこの骨組は変位法では解けない」というような意味のことをいいました。これを、ここまでの知識を踏まえて言い換えると、「この骨組の剛性マトリクスを作った時、真ん中の節点の回転方向の自由度に関する行の値が全部 0 になってしまうので、この剛性マトリクスには逆マトリクスが存在せず、変位法では解けない」ということになります。
逆マトリクスが存在するための条件というのは、じつはこれだけではありません。しかし、その数学的な証明についてここで説明してみても、(このコラムの性格上)あまり益があるとは思えません。
私たちとしては、以下のことを確認した上で次のステップに進むことにします。