2. 節点の自由度
節点変位の「ものさし」 |
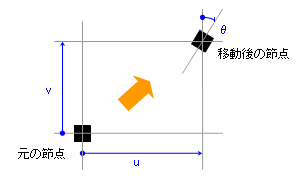
「モノがどれくらい動いたのか報告せよ」と言われたら、私たちはまず「定規」を取り出します。もし、それが二次元平面上でしか移動しないことがあらかじめ分かっているのであれば、その平面上で「横に何センチ・縦に何センチ動いた」と報告すれば済みます。これが「二次元座標系」です。
これはとても分かりやすい「変位」ですが、しかし変位法にはもう一つ、いささか分かりにくい「変位」があります。それが「回転変位」です。
節点とはようするに「点」で、これは「大きさがなく位置情報だけをもつ観念上の存在」である、といいました。だとすると、「点が回転する」というのはいささかヘンです。幾何学上の定義からすればたしかにヘンなのですが、しかしこれもすでにいったとおり、節点とは変位法というものの中で仮想された実体なのですから、「そのような属性(回転する)をもつと仮定したものが節点なのである」と考えておくしかありません。注)
注)
なぜ「回転」という属性を仮定する必要があったのかというと、それは、これが「部材の曲げモーメント」に対応するからです。したがって、部材の曲げモーメントを考慮する必要がない、完全なトラス材からなるような骨組であれば、「回転変位は考慮しない」という立場に立つ変位法もありうることになります。
だとすると、「節点がどれくらい動いたのか」を知るためには、「定規」の他に「分度器」も必要です。「時計回りに何度回転した」というような情報をそこに付け加えるわけです。
これらをまとめて図示すると下のようになります。
結論づければ、もし節点が二次元平面上でしか移動しないとするならば、その移動量は、
水平方向にどれくらい動いたか
垂直方向にどれくらい動いたか
どれくらい回転したか
という三つの「ものさし」であらわすことができる、ということになります。これを節点の 自由度 といい、上図にあるように、( u, v, θ ) という一組の記号であらわします。注)
注)
いうまでもなく、ここには無視している移動方向があります。それは「画面に垂直な方向」です。これについては「移動しない」あるいは「移動を無視する」という前提に立っていることになりますから、これを「二次元解析」または「平面解析」と呼びます。
「画面に垂直な方向」まで考える場合は「三次元解析」または「立体解析」になりますが、これはたんに「自由度が増える」というだけで、基本的な考え方が変わるわけではありません。したがって、話を必要以上にややこしくさせないために、ここでは平面解析の方だけを取り上げることにします。
節点変位が存在するための条件 |
節点変位には、水平・垂直・回転という三つの種類、つまり「自由度」があります。変位法とは、この三種類の変位量をおのおのの節点についてもとめるもので、結局もとめるべき解は「節点数×3」個だけあることになりますが、ただしここには重要な前提があります。それは、
節点変位という解がたしかに存在し、しかもその解はただ一つだけである
ということです。解が存在しないものを解くことはできませんし、解が無数に存在するのであれば、それはそもそも「問い」としての意味をなしません。
で、そのような解(節点変位)が存在するための条件とは何かというと、「節点が動こうとする時にそれに抵抗するものがある」ことです。
これはちょっと考えてみればすぐ分かります。節点がなんらかの力で押された時、最終的にどこかで静止するからその距離が計測可能になり、その距離を私たちは「変位」と呼びます。そして、なぜ節点が最終的に静止するのかというと、「節点が動こうとする時にそれに抵抗するもの」があるからです。
これを変位法の用語であらわすと下のようになります。
節点に作用する力 P と、それによって生ずる節点変位 δ は比例する。その比例定数を K とすれば、
P = K・δ
とあらわせる(これが変位法の基本式)。
ここで δ を 1 とおけば P = K なので、ようするにこの K とは「節点に単位量の変形を与えるための力」である。これを剛性という。
変位法とは節点変位 δ をもとめるものであるが、K と P が既知であれば、これは下の式で簡単にもとめることができる。
δ = P / K
そしてこの式から明らかなとおり、この δ がもとまる条件とは何かというと、それはただ一つ、「 K が 0 ではない」ことである。
いささか回りくどい言い方をしてますが、ようするに、上にいう「剛性 K」が、その前にいった「節点が動こうとする時にそれに抵抗するもの」のことです。そしてその大きさを決めるのが、節点に取り付いている「部材という実体」なのです。
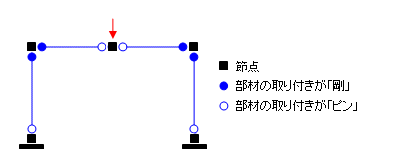
ここまで話してくれば、はじめにで取り上げた「四ピンラーメン」がなぜおかしいのか、ということは簡単に分かるはずです。先に掲げた図を、「節点とそれに取り付く部材」という観点から下のように描きなおしてみます。
上図中央の赤い矢印の節点に着目してください。この節点の垂直方向の変位に関しては左右両側の梁が片持ち梁のようにはたらいて抵抗します。水平方向の変位については左右の柱がラーメン材として抵抗します。しかしもう一つの変位、「回転」についてはどうでしょうか?
この節点の両側に取り付く梁がともに「ピン接合」なので、この節点が回転しようとする時に「それに抵抗するもの」が何もありません。つまり剛性が 0 なので、この節点には回転変位という解が存在しないことになります。だからこの骨組は変位法では解けないのです。
これには以下のような反論があるかもしれません。
この節点に対する部材の取り付きはピンなのだから、部材の曲げモーメントは 0 である
だから、この節点の回転変位がどうであろうと関係ないはず
だったらこれでもいいんじゃないの?
しかし、もしそうであるのならば、設計者は、「この節点については回転変位をもとめる必要がない(つまり回転変位は拘束されている)」ということをあらかじめ変位法の側に指示しておく必要があります。なぜなら、「この節点の回転変位は関係なさそうだからもとめなくてもいいや」と変位法の側が気を利かしてくれるわけではないからです。注)