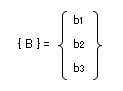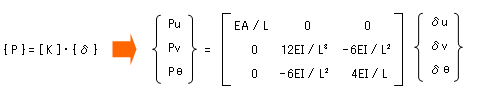5. マトリクスとは? (その1)
マトリクスとベクトル |
数学用語としての Matrix の訳語は「行列」ですが、しかし、どちらかといえばカタカナ表記の「マトリクス」の方が多く使われています。注)
注)
一時期までは「マトリックス」のように促音「ッ」を入れて表記されるのが一般的でしたが、だんだんと「マトリクス」の方が優勢になってきているようなので、ここでもこちらの方を採用することにします。もっとも、映画の題名は「マトリックス」となってましたが・・・。
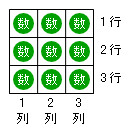
マトリクスというものを手っ取り早く理解したいなら、下図にあるような、オセロゲームの桝目の中にオセロの駒のかわりに数字が入っているような状態を想像すればいいでしょう。
この桝目の横の列を「行」と呼び、上から 1 行 2 行・・・と数えます。縦の列を「列」と呼び、左から 1 列 2 列・・・と数えます。ようするに、「行」と「列」からできているので「行列」である、ということです。注)
注)
縦であれ横であれ、どちらも「数字のならび」であることに違いはないのですから、一般的な語法では「縦列」「横列」とするべきものでしょう。
そもそも日本語の「行」にも「列」にも「縦か横か」という情報は含まれていません。私自身のことをいえば、「どちらかといえば縦のならびを行と呼ぶはず」という先入観があって、「横のならびを行と呼ぶ」には少なからず違和感があります(日本語は本来縦書きにするものなので、私たちにとっては縦のならびを一行二行と数える方が自然だと思うのですが、違うでしょうか?)。
まあしかし、表計算ソフトなどでも「横が行・縦が列」という呼び方はすっかり定着していますので、それに慣れるしかありません。ちなみに、行は row、列は column の訳語です。
マトリクスを使うと、その中にある個々の数値(これをマトリクスの要素と呼びます)をいうかわりに、それらを一まとめにして「このマトリクスなにがしは・・・」ということができるようになります。
さきほどはオセロゲームにたとえましたが、ゲーム盤を教室に見立て、桝目の一つ一つを教室に並んだ机だと考えてください。机にはそれぞれ生徒が一人ずつ座っていて、名前も顔もみな違っていますが、ここでは、その生徒一人ずつの名前を読み上げるかわりに「三年一組」という呼び方をすることができるのです。これはなにかと便利に違いありません。
それがマトリクスであることをしめすためには、その呼び名を [ ] で囲んで [ A ] のように書きます。
たとえば 3 行 3 列のマトリクスの場合、下図にあるように、そのマトリクス [ A ] には計 9 個の数値が入っていることになります。(ここにあるとおり、それが m 行 n 列の要素であることをしめす場合、変数名の後に mn という添え字を付けてあらわす習慣があります。)
さらに、マトリクスの仲間に「ベクトル」というものもあるので、こちらも憶えておいてください。
下図にあるとおり、これはようするに「一列しかないマトリクス」のことで、こちらはその呼び名を { } で囲んで、{ B } のように書きます。注)
注)
「一列しかないマトリクス」があるのなら、当然、「一行しかないマトリクス」だってあります。これを区別する場合には前者を「列ベクトル」・後者を「行ベクトル」と呼びますが、変位法でたんに「ベクトル」といった場合は「列ベクトル」のことを指します。
それからもう一つ、「一列しかないマトリクス」があるのと同様に、「要素が一つしかないベクトル」というのもあります。これを「スカラー」と呼びます。ようするにこれは、私たちがいつも使っている「数」のことですね。
マトリクスとベクトルの掛け算 |
マトリクスもベクトルも複数の数値を一まとめにしてあらわしたものですが、しかし、ただそれだけのことなら別にどうということもありません。肝心なのは、マトリクスとベクトル、あるいはマトリクスどうしの「掛け算」ができる、という点にあります。これは、さきほどのたとえを使えば、三年一組と三年二組を掛け合わせて三年X組という新しいクラスを作るようなものです。
ただし、これが普通の掛け算とは違うのは、「掛けるもの」と「掛けられるもの」の間に必ず一定の「相性」が必要になる、という点です。それがどういう相性なのかを知るために、まず「マトリクスとベクトルの掛け算」から始めることにします。
ここにある最初のルールは、
マトリクスとベクトルの掛け算は、かならず「マトリクス×ベクトル」という順序になる
というものです。つまり、[ A ] × { B } はできても { A } × [ B ] はできないのです。
もう一つのルールは、
マトリクスの列数とベクトルの要素数はひとしくなければならない
というもので、さらには、
そのようにして掛けられた結果は、マトリクスの行数とひとしい要素数もつベクトルになる
というのだってあります。
しかし、これでは何のことかさっぱり分からないと思いますので、マトリクスとベクトルの掛け算の様子をあらわした下の図を見てください。
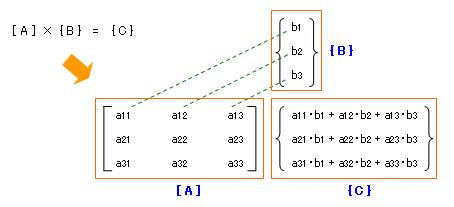
これは [ A ] × { B } = { C } という演算の様子をあらわすために、[ A ] の右上に { B } を書き、右下に { C } という結果を書いたものです。図中の破線が具体的な掛け算をあらわしています。
ようするに、得られた { C } というベクトルの最初の要素は、[ A ] の 1 行目の各列の要素に { B } の各要素を順番に掛け合わせたものの合計で、二番目の要素は、同様に、[ A ] の 2 行目の各列の要素に { B } の各要素を順番に掛け合わせたものの合計です。
これを見れば、さきほどのルール
マトリクスの列数とベクトルの要素数はひとしくなければならず、そのようにして掛けられた結果は、マトリクスの行数とひとしい要素数もつベクトルになる
の理由も納得していただけるはずです。
では、どうしてこんなヤヤコシイ掛け算を考え出したのかというと、それはもちろん、このルールにもとづくと、いろんなことが合理的にあらわせるからなんです。
マトリクスとベクトルによる変位法の基本式 |
変位法の基本式が P = K・δ である、ということはもう何度もいいました。そして前回取り上げた片持ち梁の例では、この基本式の中身が下のようになることを確認しました。
Pu = ( EA / L )・δu
Pv = ( 12EI / L3 )・δv - ( 6EI / L2 )・δθ
Pθ = ( -6EI / L2 )・δv + ( 4EI / L )・δθ
基本式 P = K・δ の中身が上のようになっている、ということは、この P はじつは( Pu, Pv, Pθ )という三つの値の総称であり、δ はじつは(δu, δv, δθ )という三つの値の総称である、ということです。つまり、これは { P } あるいは { δ } のようにあらわせる「ベクトル」なのです。
この { P } を外力ベクトル、 { δ } を変位ベクトルと呼びます。
そして、この間を取り持っている K の方はどうなのかというと、これがじつは「マトリクス」です。したがって、これを [ K ] のようにあらわし、剛性マトリクスと呼びます。
これがどのようなマトリクスなのかを知るために、さきほどの式を、わざと「係数 0 」を使って下のように書き換えてみます。
Pu =
( EA / L )・δu +
0・δv +
0・δθ
Pv =
0・δu +
( 12EI / L3 )・δv +
( -6EI / L2 )・δθ
Pθ =
0・δu +
( -6EI / L2 )・δv +
( 4EI / L )・δθ
これらの式と、前項に述べた「マトリクスとベクトルの掛け算」の図を重ねあわせると、結局、この場合の変位法の基本式は下のようにあらわせることになります。
ところで、外力ベクトルと変位ベクトルの要素数はともに「その骨組の自由度の総数」です。ということは、これらの仲立ちをしている剛性マトリクスは、「行数と列数がともに自由度の総数に等しい」マトリクスでなければならないはずです。
このような、同じ行数と列数をもつマトリクスのことを正方マトリクスと呼びます。つまりこういうことです。