保有水平耐力をいかにもとめるか

前回話した、各階のエネルギー分配量を決めるための指数 pi の中には「各階の保有水平耐力 Qui 」という項が入っていました。つまり、エネルギー法でも「保有水平耐力」の値が必要になるのですが、安全限界の検証が建物の塑性化を前提としている以上、これはアタリマエの話です。
現在、建物の保有水平耐力は「増分解析」によってもとめるもの、という考え方がなかば常識化しています。しかし、この方法によって各階の保有水平耐力をまんべんなくもとめることができないケースがあります。いわゆる「層崩壊メカニズム」の建物で、その典型的な例をあげれば、下に掲げるピロティ建築物のようなものです。

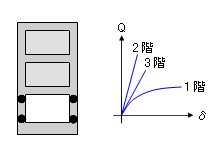
今さら言うまでもないかこともしれませんが、このような建物では、他の階に先立って建物の 1 階だけが崩壊してしまうため、この時点での 2 階ないし 3 階の層せん断力を「保有水平耐力」とすることはできません。この時点でまだ崩壊に至っていないのですから、本当の保有水平耐力はこれよりも大きいはずです。
しかし、保有水平耐力計算や限界耐力計算では、（多少の留保はつくものの）「これを保有水平耐力と見なしても構わない」とされます。これはどういうことかというと、「本当の保有水平耐力よりも小さな値を採用することは結果的に安全側の評価になる」からです。
一方、エネルギー法では、そのような立場をとることは許されません。なぜなら、

保有水平耐力計算や限界耐力計算では保有水平耐力の大小が直接問題になるが、エネルギー法では、保有水平耐力そのものの大きさではなく、その値の各階における相対的な比だけが問題にされる

からですが、このあたりの事情は前回に話したとおりです。

ただし下図のように、「 Ai 分布にもとづく外力分布」を作用させた増分解析において、建物全体が梁降伏型の崩壊メカニズムになり、その状態が各階の「本当の保有水平耐力」をあらわしているのであれば問題はないことになります。この時の各階の保有水平耐力の分布は「 Ai 分布にもとづく層せん断力分布」と相似になりますので、前回話した pi の値は 1 もしくはそれに近い値になるはずです。

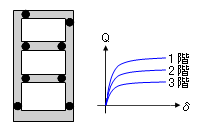
そこで問題は、先に掲げたような層崩壊メカニズムになる建物の保有水平耐力をいかにしてもとめるか、になるわけですが、たとえば、個々の層ごとに架構を分解して個別に増分解析を行う、という方法もないわけではありません。しかし、そもそもコンピュータプログラムを使わずに増分解析を行うことはできませんし、また、そのような特殊な解析法を組み入れたプログラムが一般に流通しているのかというと、実際のところ、あまり聞いたことがありません。つまり、そのような解析を行える立場にある人はごく限られているはずです。

そこで思いつくのが、「節点振り分け法」というアイディアです（ただし、鉄骨造、あるいは耐震壁のない ＲＣ 造の建物に対象が限定されますが）。^注）
たしかに、エネルギー法がもとめている保有水平耐力とは、節点振り分け法から得られる崩壊メカニズムにもとづいた値に近いものである、と言うことができそうです。ただしここには、「節点モーメントをどのように振り分けて層せん断力をもとめるか」という問題があります（これについても前に話しました）が、この点さえ何らかの方法でクリアーできれば、節点振り分け法がエネルギー法における有力なツールになることは間違いないでしょう。

注）
限界耐力計算は、明らかに「増分解析」を前提にしたものです。その証拠に、2007 年の基準法改定の折に、限界耐力計算関連告示の中に「増分解析により行う」という一文が追加されました。しかし、エネルギー法と増分解析の間に直接的な関連性はなく、「保有水平耐力をいかにもとめるか」に関する規定もありません。
それからもう一つ、これはまったくの余談ですが、公開中のプログラム「ビルディング・エディタ Ver.5.1 」に「エネルギー法」の検証機能を追加すると同時に「節点振り分け法」による保有水平耐力の計算機能を追加したのは、ここに述べているような理由からです。