節点振り分け法

しかるべく設計され、しかるべく施工された建物に大きな力が作用して壊れる場合、たいていはその「端部」から壊れていきます。真ん中から壊れる、ということはまずありません。これは、柱なり梁なりの力学的な性状として、その端部にもっとも大きな力が集中するような仕組みになっているからです。

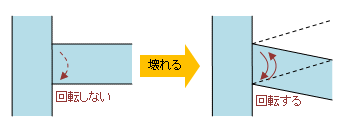
で、その「壊れる」とは何なのかというと、梁が柱に、あるいは柱が梁にリジッドに結合されている状態から、その結合が「ゆるむ」あるいは「ほどける」状態のことをいいます。
結合がほどけた後どうなるかというと、そこに「ちょうつがい」ができたような状態になり、「回転能力」が生まれます。
そんなことから、この状態を「ヒンジ（hinge = ちょうつがい・関節）が発生する」と呼びます。

ところで、いま「部材が壊れる」と言いましたが、この表現はいささか厳密さを欠いています。工学的な表現によれば、ヒンジができるのは「降伏（弾性限界を超える）する」で、「本当に壊れる」のは「破壊する」です。
この「破壊」とは何かというと、ヒンジ、つまり「ちょうつがい」そのものが壊れて機能を果たさなくなった状態（部材の最終状態）のことです。したがって、たんにヒンジができただけならば、その部材は「まだ壊れていない（破壊にまでいたっていない）」と言います。
なぜならば、ヒンジができたからといって、梁が落ちてくるわけでも、柱がつぶれてしまうわけでもなく、依然として、「鉛直方向の荷重を支える」という部材本来の機能を保持しつづけるからです。

そのような意味において、これは建物の「健全な壊れ方」である、とされます。
しかるべく設計され、しかるべく施工された建物ならばこのような壊れ方をするはずですが、もちろん、その一方には「不健全な壊れ方」というものも存在します。が、話を先に進めるため、ここでは「しかるべく設計された建物が健全に壊れていく」話に限定することにしましょう。

いま申し上げたとおり、部材にヒンジができても、それがただちに部材の最終状態（破壊）につながるわけではありません。しかしその一方、これを建物、つまり「部材の集合体」という観点から見るならば、そのあちこちに新しいヒンジ（関節）ができてくることによって全体の剛性が少しずつ失われていきます。
そしてついに、ある限度以上のヒンジができると、もはや建物としての力学的なメカニズムを保持することができなくなってしまう・・・この状態を建物の「崩壊」といいます。

さて、ここで大事なのは、「ヒンジが作られて建物が崩壊する」ではなく、「ある一定限度以上のヒンジが作られない限り建物は崩壊しない」の方です。

先に、1981 年制定の「新耐震設計法」というものにふれましたが、それまで行われていた設計手法（現在の一次設計に相当するもの）は「中規模の地震（震度 5 程度）に対して建物に 1 個のヒンジも作らせないようにする」ものでした。では、それを超えるような大規模の地震（震度 6 程度以上）に対してどのように対処したのかというと、じつは「何もしなかった」のです。
何もしなかった理由というのが、他でもない、上に述べた事実にあります。
つまり、

建物に最初のヒンジが発生してから、建物の崩壊にいたるに十分な数のヒンジが形成されるまでには多くのステップが必要である。
だから、中規模の地震に対して 1 個のヒンジもできないように建物を設計しておけば、大規模の地震がきても、それが多くのステップをクリアーし、十分な数のヒンジを形成して建物を崩壊にいたらしめることはほとんどない（その事実はこれまでの震災経験からも実証されている）。

という立場をとっていました。
いわば、建築構造物というシステムの「冗長性」に期待したわけです。
これに対し、経験知にたよることなく、建物が崩壊にいたるメカニズムを追跡して検証しようとしたのが「新耐震設計法」であり、「保有水平耐力計算」なのです。

となると、最初の問題は「いったい何個のヒンジが形成された時に建物は崩壊するか」ですが、これについて力学的な手続きで簡単に求めることができます。いちばんの問題は「どこにどういうふうにヒンジが形成されるか」です。
そこで、以下のような巧妙な仮定を立てることにしました。

節点位置において、柱の最大耐力と梁の最大耐力を比較し、耐力の小さい方の側（柱の側あるいは梁の側）にヒンジが形成される。

上にある「節点（せってん）」とは「柱と梁が集合する場所」のことで、下図の例でいえば、この建物には計 9 個の節点が存在することになります。
ここには、最大で 2 個の柱と 2 個の梁が接続することになりますが、これらのすべての節点で、柱の耐力の和と梁の耐力の和とを比較し、どちらか弱い方の側にヒンジを作っていくと下図右側にあるような状態が出来上がります。
で、これだけの数のヒンジが形成されると、建物は必ず崩壊するのです。

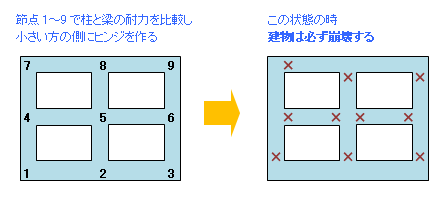
上図の節点 2 や 8 のように「柱 1 ： 梁 2」の場合はたいてい柱の方が劣勢なので柱の側にヒンジが作られます。逆に、節点 4 や 6 のように「柱 2 ： 梁 1」の場合はたいてい梁の側にヒンジが作られます。
節点 5 のように「柱 2 ： 梁 2」の場合は比較によりますので一概にはいえませんが、ふつうに設計された建物では柱の耐力の方が大きくなる（柱の方が「余力」がある）傾向があるので、たいてい梁の側にヒンジが作られます。これを「梁降伏」といい、逆に柱の側にヒンジが作られる場合を「柱降伏」といいます。
（もちろん、どちらか 1 本の梁とどちらか 1 本の柱にヒンジが作られる、ということだって実際には十分ありえますが、ここでは「そういう状態は考えない」ことにしているのです。）

以上が「節点振り分け法」と呼ばれる計算手法のあらましですが、これの一番の利点は「電卓があれば計算できる」ことです。
「保有水平耐力計算」が手法として確立された 1980 年代の初めは、「構造計算は電卓を使ってするもの」とされていた時代ですから、当然ながら、保有水平耐力計算の細則はこの「節点振り分け法」を前提に作られました。そして、その基本的な枠組は今でも変わっていないのです。

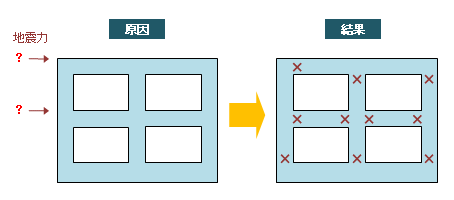
ところで、この方法によって得られるヒンジの形成状況というのは、いってみれば結果に過ぎません。その結果をもたらす原因となるのは、いうまでもなく「地震による力」です。その大きさを特定しないことには「この建物がどの程度の地震力に耐えうるのか」が分りません。
そこで、次に、「結果から原因を特定する」という作業が必要になってくるわけです。

たとえば結果が 5 で、その原因となる項が一つしかないのであれば話は簡単で、5 = 5 しかありません。しかし、原因となる項が二つだとすると、それは 2 + 3 かもしれないし、 1 + 4 かもしれない。つまり、 5 という結果をもたらす原因は無数に存在するのです。
これを建物の話に戻すと、平屋の建物なら問題ないが、2 階建て以上の建物になると、結果として得られた「建物の崩壊状態」をもたらす原因、つまり「各階に作用している地震力」の値を一義的に定めることができなくなくなる、ということです。

では、どうしたらいいのか？
実際のところは、どうしようもありません。
そもそも「結果からその原因をもとめる」という手法自体に本質的な限界があるためで、せいぜいできるのは、「建物の地震力の分布としてあまり不自然にならないようなものにしておきましょう」くらいのことです。そのあたりのテクニックが「節点振り分け法」という名称の「振り分け」の部分になるのですが、ここでは、その説明は省きます。

そういうわけで、「原因（地震力の分布）から結果（建物の崩壊状態）を得る」というオーソドックスな手法がコンピュータの高性能化・大衆化とともに保有水平耐力計算の主流になってくるのですが、その前に、「地震力の分布」というものについて復習しておきます。