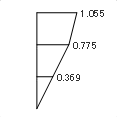|
Ai 分布の精算について - 2 -
Ai 分布の精算に使うのは「応答スペクトル」「モード合成法」――黄色本には「モーダル・アナリシス」とあるが、同じもの――という二つのツールです。
手短に言えば、応答スペクトルとは、建物に「ある地震波」が作用した時にどのような応答 ( 変位・速度・加速度 ) が生じるかを簡単に推定するためのものです。この時、建物の応答はその固有周期に依存するという性質があるため、応答スペクトルの横軸は建物の固有周期、縦軸が応答値 ( ここで使うのはもっぱら加速度応答値 ) になっています。
私たちに最も馴染みがある応答スペクトルは「振動特性係数 Rt 」でしょう。
この値は立地の「地盤種別」ごとに定められていますが、これは「建物に作用する地震波の性状は立地地盤の性状 ( 固有周期 ) に依存する」という前提――建物の揺れ方がその固有周期に依存するのと同じ――によるものです。
下図がこの値を表わしたグラフですが、ただしこの値は応答加速度を直接的に指したものではなく、最大値を 1.0 として規準化されています。ですから、対象とする地震波の最大加速度がたとえば 200 ガルであるのならば、1.0 の線を 200 ガルというふうに読み替える必要があります。
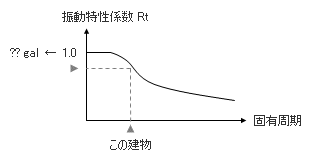
もし、この建物が平屋建て ( = 1 質点系 ) であるのならば「これで終わり」です。そもそも、平屋の建物に Ai 分布は必要ありません。
一方、多層の建物 ( = 多質点系 ) の場合、まず問題になるのは「固有周期が複数ある」ことです。
一般に n 質点系 ( n 層の建物 ) には n 個の固有周期があり、そしてさらに、私たちは n 個すべての質点についての応答を知る必要がある――これがまさに「 Ai 分布」なわけです。
ところで、ここには以下のような法則があります。
n 質点系には必ず n 個の「固有モード」( = 振動形 ) があり、この質点系の応答は、これらを適切に合成すれば求めることができる
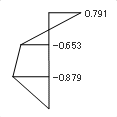
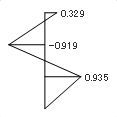
上に述べた「 n 質点系には必ず n 個の振動形があり、それ以上でも以下でもない」という事実を、下に示した簡単な 2 質点および 3 質点系の例で確認してください ( なお、質点系は「左右に揺れる」ので、この図を左右反転させたような振動形は「同じ一つのもの」と考えます ) 。
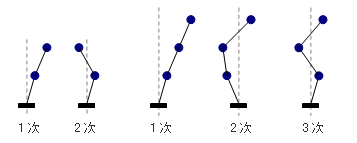
これらの固有モードは「固有周期」という値とセットになっていて、それぞれ「 1 次固有周期 ( 固有モード ) 」「 2 次固有周期 ( 固有モード ) 」… のように呼ばれます。
1 次の固有モードは「すべての質点が同じ方向に一方的に揺れる」という最も単純な形です。そして次数が上がるにつれて複雑な振動形――具体的には、振動形が中心線を横切る数が一つずつ増えていく――になる。さらにここには、「 1 次の固有周期が最も長く、次数が上がるにつれて短くなる」という性質もあります。
固有周期や固有モードは質点系の「質量」と「剛性」から計算できるのですが、ここではそれらの具体的な計算方法は省き、以下、具体的な例題を使いながら説明することにしましょう。
下にあるのは、ある実在の建物 ( 3 階建て ) について計算した固有モードと固有周期の値です。
| - |
1 次 |
2 次 |
3 次 |
| 固有モード |
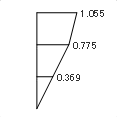 |
 |
 |
規準化した
固有モード |
2.857
2.098
1.000 |
-0.900
0.743
1.000 |
0.350
-0.982
1.000 |
| 固有周期 (秒) |
0.323 |
0.123 |
0.085 |
| 刺激係数 |
0.440 |
0.363 |
0.197 |
まず一番上の行の「固有モード」ですが、ここにある値は何らかの具体的な量――変位とか加速度とか――を直接表わしたものではありません。これは無次元量で、さらに、ここで問題になるのは値そのものの大小ではなく、各質点間における値の相対的な「比」だけになります。
そこで、値の比較を容易にするために「規準化」という処理がよく行われます ( 別に「そうしなければいけない」というわけではありませんが ) 。どこかの値を 1 とし、他の質点についてはそれに対する比で表わすことにしますが、表の二番目の行にある「規準化した固有モード」は一番下の質点の値を 1 としたものです。
表の一番下にある「刺激係数」とは一体何でしょうか ?
どうも、この「刺激」という言葉に惑わされてしまいますが、これは paticipation factor の訳語で、「影響度係数」とでも訳した方が分かりやすい気もします。ようするに、質点系全体の応答に及ぼす各次モードの「影響の度合い」を表わした指数です。その算定式は略しますが、この値が大きいほど「その次数のモードが全体に与える影響が大きい」ことになります。
当然ながら、この値は 1 次モードで最も大きく、次数が上がるにつれて小さくなる ( たんに「建物の固有周期」という場合、それが「一次固有周期」を指すということを思い出してください ) 。したがって、この値が小さければその次数の影響はほとんど無視できることになりますが、一般に、高層の建物であっても 3 次モードくらいまで考慮しておけば実用的には十分であるとされています。
これだけの準備をしておいて、いよいよ「応答値」を求める手順に入ります。
ここで「応答スペクトル」が登場するのですが、ここから得られるのは「 1 質点系の応答値」に限られます。そこで、まず多質点系を「各次数の固有周期を持った 1 質点系」に分解することにします。その上で各次数の応答値を求めれば、「多質点系の応答は各次モードの合成によって求められる」の原理にしたがって全体の応答が得られそうな気がします。
この時に、応答スペクトルの代用として「振動特性係数 Rt 」を使うことは先に述べた通りです。
本例では 1 次固有周期でも 0.323 秒しかないので、地盤種別に関係なく、すべての次数において Rt は 1.0 になります。だから応答加速度 1 ガルということで構わないのですが、これではちょっと現実味に欠けるので 200 ガルということにしておきましょう ( 加速度の大きさそのものを問題にしてるわけではないので、このあたりは何でもいいのです ) 。
ところで、この「各次数に分解された 1 質点系」とは何なのかというと、「その次数の固有モード ( 振動形 ) を保ったまま揺れている仮想の 1 質点系」と考えられます。したがって、この時の各質点の応答値は、
その質点の固有モード値 × 刺激係数 × 仮想された 1 質点系の応答値
で得られます ( ここまで固有モードのことをしばしば「振動形」と呼んでいたので誤解されるかもしれませんが、弾性範囲内では変位と加速度は比例しますので、固有モードとは変位を表すと同時に加速度の分布も表わした値なのです ) 。
たとえば 1 次モードの一番上の質点については 2.857 × 0.440 × 200 = 251.4 ガルが応答値です。同様にしてすべての次数のすべての質点について応答値を計算すると下のようになります。
| - |
1 次 |
2 次 |
3 次 |
| 加速度 |
251.4
184.6
88.0 |
-65.3
53.9
72.6 |
13.8
-38.7
39.4 |
加速度に質量を掛けたものが「力」ですから、上の値に各質点の質量を掛けたものが地震時の外力ですが、ここでは話を簡単にするために、質量をすべて 10 ( 9800kN に相当 ) としておきましょう。すると以下のように各質点に作用する外力 pi が得られます。
| - |
1 次 |
2 次 |
3 次 |
| 外力 pi |
2514
1846
880 |
-653
539
726 |
138
-387
394 |
これで「各質点 ( = 各階の床位置 ) に作用する地震力 pi 」の値が分かりましたから、本来は「これで終わり」でもいいはずですが、そうはいかないのが現行基準のややこしい所です。
Ai という値は「外力の分布」ではなく「層せん断力の分布」を表わしたものなのです。そこで次に、pi を上から足し合わせて各階の層せん断力 Qi を下の左側のように求めることにします。
| - |
1 次 |
2 次 |
3 次 |
層せん断力
Qi |
2514
4360
5240 |
-653
-114
612 |
138
-249
145 |
|
→ |
Qi の最大値
( 絶対値の和 ) |
3305
4723
5997 |
|
上の右側にあるのは、各質点の 1 次・ 2 次・ 3 次の応答値の絶対値を単純に足し合わせて「各質点の Qi の最大値」としたものです。
しかし、「各次数の最大値を単純に足し合わせる」というのはちょっと変ですね。というのも、各次の固有周期が違えば「揺れ方」が違うのですから、一般に、各次の最大応答値が同時に発生することはないと考えられるからです。これを「同時」と見なすことは設計値として「過剰 = 安全側過ぎる」のです。
そこで、もう少し「それらしい値」を求める方法が求められるのですが、黄色本では SRSS という手法を推奨しています。これは日本語にすると「二乗和平方根」で、「各次の最大値を二乗したものの和の平方根をとる」という考え方です。
たとえば本例の一番上の質点を例にとると、二乗和は 25142 + ( -653 )2 + 1382 = 6340546 で、その平方根は 2601 です。他の質点についても同様にして求めると下の左の表のようになります。
( ただし、これはあくまでも「各次モードの最大値が独立して生起する」という仮定の下での推定値ですので、各次の固有周期の差が小さく、最大値が「ほぼ同時」に起きると考えられるようなものでは値が過少になります ) 。
Qi の最大値
( SRSS ) |
2601
4368
5277 |
|
→ |
| Qi / Σ mi |
260.1
218.4
175.9 |
| → |
|
上の中ほどにあるのは、左側で求めた Qi を質量の和 ( 上から 10 ・ 20 ・ 30 ) で割った、いわば「疑似的な層せん断力係数」の値です ( もちろん、本来は「重量」で割るべきですが、ここでは各階の相対的な比だけが問題なので、便宜的にこうしています ) 。
そしてこの値を最下階で 1 になるように規準化すれば、上の一番右にあるような「 Ai 分布」の値がめでたく得られることになります ( 参考までに、固有周期 0.323 秒として略算により求めた Ai の値は、上から 1.46・1.18・1.00 です ) 。
前へ | 1 | 2 |
( 文責 : 野家牧雄 )
|