8. 骨組の支持条件
支持条件の導入 |
これまでは、もっぱら片持ち梁の例を取り上げ、その剛性マトリクスを何度も引き合いに出しながら説明を進めてきました。
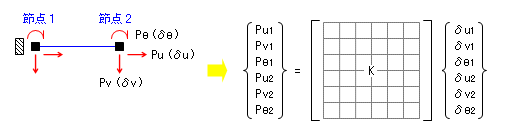
ただし、これまで引き合いに出してきた剛性マトリクスは、正確にいえば「片持ち梁の先端の節点にかんするもの」です。しかしご存知のとおり、片持ち梁のもう一方の側(固定端)にだって「節点」はちゃんとあります。
つまり、ここには節点が二つあるのですから、一方を「節点 1 」・他方を「節点 2 」とすれば、この場合の変位法の基本式は、本来は下のようなものでなければならないはずです。
でも、これを解くことはできません。この 6 × 6 の剛性マトリクスには「逆マトリクスが存在しない」のです。なぜか?
答えはいたって簡単で、この梁は「宙に浮いている」から、言い換えれば、「梁の一方の端部が固定されている」という条件がここにはまったく入っていないからです。
私たちはよく「支点」という言い方をしますが、これは「変位が拘束されている節点」のことであり、べつの言い方をすれば「変位量が 0 になることがあらかじめ分かっている節点」です。
一方、変位法とは「節点変位をもとめる方法」ですが、最初からその値が 0 になることが分かっているのだったら、それをわざわざもとめる意味はありません。また、「支点に作用する外力」というのも同様に何の意味ももちません(「動かない」と最初から分かっているものをいくら押してみてもしょうがない、ということ)。
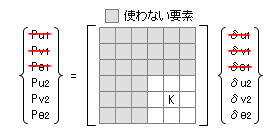
上の例でいえば、固定端を「節点 1 」とすると、変位が 0 になるのは ( δu1, δv1, δθ1 ) の三つで、これに対応する外力が ( Pu1, Pv1, Pθ1 ) の三つです。当然、これらの変数に関与する剛性マトリクスの要素は使われることがありませんから、意味をもつ剛性マトリクスの要素は下 3 行と右 3 列だけです。結論としては、下にしめすような 3 × 3 の剛性マトリクスだけを考えておけばよい、ということです。
上図にある 3 × 3 の剛性マトリクスこそが、じつは、今までさんざん引き合いに出してきた「剛性マトリクス」の正体です。
もちろん、この剛性マトリクスには逆マトリクスが存在します。これは何かというと、最初に掲げた 6 × 6 の剛性マトリクスに適切な支持条件を導入して 3 × 3 にサイズダウンさせることによって「安定骨組の剛性マトリクス」になった、ということを意味しています。
支点反力のもとめ方 |
しかし、上に述べた方法にはひとつ欠点があります。このやり方では「支点反力」がもとまらないのです。
これはよく考えてみれば当然のことで、支点反力が生じるような節点なり自由度なりの項を最初から消してしまっているわけですから、その自由度について何かの情報が得られるはずもありません。そもそも、「部材」も「バネ」も存在しないところで「力」をもとめようとしても、それは無理な話です。
にもかかわらず、たいていの応力計算プログラムは「支点反力」というものをちゃんと出力してきます。これは一体どうやってもとめたんでしょう?
たいていの場合はどうやっているのかというと、仕方がないので、「変位法による計算が終わった後で、支点に集まっている部材の内力を集計して」もとめています。支点に集まる部材の内力の和と支点反力は釣り合うはずですから、これはこれで正しいのですが、しかしそれにしても、支点反力だけは、変位法の計算プロセスとはまったく関係のないところで「後から」計算していることになります。
そこで、「変位法の計算プロセスの中で支点反力をもとめる方法はないものか」となりますが、ないわけでもありません。
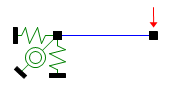
支点の部分を「完全に固定されている」のではなく、「テキトーに大きな剛性をもったバネが付いている」と考えるのです。さきほどの片持ち梁についていえば、下のようなモデルです。注)
注)
もっとも、市販の応力計算プログラムでこのようなモデルで支点反力をもとめているものがあるかというと、おそらくないと思います。たいていのプログラムは、先に述べたような「後からもとめる」という方法をとっているはずです。
ここでこういう話を持ち出すのは、「このような考え方もできるのだ」ということを知ってもらうことと、それを知ることが変位法そのものの理解に多少とも役立つのではないか、と思うからです。
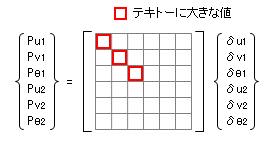
このモデルは剛性マトリクス上でどのようにあらわされるのかというと、冒頭にしめした 6 × 6 の剛性マトリクスの支点に相当する行(上から 3 行)の対角要素にこのバネの剛性、つまり「テキトーに大きな値」が入った状態になります。
さきほど、この 6 × 6 のマトリクスには逆マトリクスが存在しないので解けない、といいましたが、上のような操作を加えると、ちゃんと解けるようになります。なぜなら、これによって「固定支点が存在するのと同等の状態」になるからです。
これを解けば、支点の変位量( δu1, δv1, δθ1 )が得られます。これはもちろん「非常に小さな値」のはずですが、これにさきほどの「テキトーに大きな剛性」を掛ければ、それが支点反力( Pu1, Pv1, Pθ1 )である、ということです。このような方法を使えば、「変位法のプロセス内で支点反力をもとめる」ことができます。注)