|
モバイル版およびデスクトップ版の「かんたん平面板」というアプリを公開中ですが、「線材はともかく、面材の応力はどうも...」という声をしばしば耳にします。「主応力とは何か ?」という質問もありました。 たしかに、一般の建築構造技術者が日常業務で面材の応力に出会うのは、ここで扱っている「床スラブの曲げモーメント」くらいかもしれません。 このアプリで使っているのは「有限要素法」と呼ばれる解析手法ですが、しかし後ほど取り上げるように、これで板の曲げモーメントを求めるのは有限要素法の「応用問題」みたいなものです。 そこで一般的な有限要素法を理解するために、下図①のような「片持ち梁」を考えてみます。 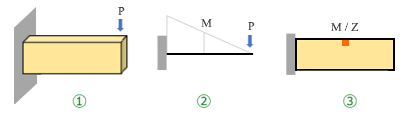 一般的な建築構造計算では、これを図②にあるような「線材」に置き換えます。この線にいくつかの属性 ( ヤング係数・断面性能など ) を与えれば、先端の変位量や任意位置の曲げモーメントを公式で簡単に求めることができる。 さらに、部材断面の安全性を検証するには応力度 ( = 単位面積当たりの力 ) の値も必要ですが、これも公式を使えば簡単です。曲げモーメント M を部材の断面係数 Z で割るだけ ( 図③ ) 。 つまりここでは、面材をいったん線材に置換した上で、最後は再び面材に戻しているわけですが、有限要素法とは、これを最初から最後まで「面」として扱うものです。とは言え、梁全体を一つの面材として扱うことはできないので、これを小さな面材 ( 要素 ) に分割し、その集合と考えます。 ところで、今しがた「応力度」と書きましたが、これについては注意が必要です。 この文章は、建築構造技術者向けに有限要素法のアウトラインを紹介することを目的としますが、「応力度 = 単位面積あたりの力」という用語法は建築方面に独特のもので、材料力学の分野ではにこれを「応力」と呼びます ( これに対し、さきほどの曲げモーメント M のようなものは「内力」 ) 。 したがって、以下では、私たちが日常的に「応力度」と呼んでいるものを「応力」と書いていることに注意してください。 話を戻しますが、ご存じの通り、曲げを受ける梁の応力は断面内に一様に分布するわけではありません。材質が均一であれば、下図左にあるように、中立軸をはさんで引張側および圧縮側に反転して分布します。これは中立軸からの距離を変数とするアナログ量です。 これに対し、有限要素法の解は「各要素の応力」というデジタル量で、その値は下図右のような状態で「とびとびに」に得られます。 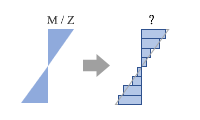 このどちらが「正解」なのかというと、それは左側、つまり線材に置換した上で公式から求めたものです。有限要素法で得られるのは「近似解」に過ぎません。 ですから、構造物を線材に置換し、その性質を線材の属性として過不足なく盛り込むことができるのであれば線材として扱うのが妥当だし、明快です。そもそも手間もかからない。 しかし、梁の途中に切り欠きがあったり、孔があいているような場合はどうでしょう ? これを単純な線材として扱うのは少々無理がある。そこで「有限要素法」の出番になるわけです。 有限要素法の「要素」 有限要素法には FEM という略称があります。これは Finit ( 有限 ) Element ( 要素 ) Method ( 法 ) の略で、読んで字の如し。ようするにこれは構造物が何らかの外力を受けている時、その対象を複数の要素に分割した上で各要素に生じている応力を求める方法です。 となると問題は「どういう要素に・どのように分割するか」ですが、まず「どういう」について言えば、以下の三つに大別されます。 ・線要素 ← 「棒」のような構造物 ・二次元平面要素 ( シェル要素 ) ← 「板」のような構造物 ・三次元立体要素 ( ソリッド要素 ) ← 「かたまり」のような構造物 最初の「線要素」は建築構造計算でおなじみのものです。 私たちは複数の線 ( 部材 ) で構成された構造物 ( 骨組 ) の応力を「変位法」あるいは「剛性マトリクス法」などと呼ばれるやり方で解いていますが、これは有限要素法の仲間です。違うのは、対象が「線」か「面」かだけ。基本的な考え方は変わりません。 二番目の「平面要素」は「かんたん平面板」で扱っているもので、先に書いたように「板と見なせるもの」が対象です。この前提が成立しないものについては三番目の「立体要素」を使うことになる。 それにしても、「板と見なせる」とは何なんでしょうか ? しばしば言われるのは、その厚さが辺長 ( 短い方 ) の 1/20 以下であれば「板」である、ということ。この数字の根拠はよく知りませんが、ただしこの制限から外れていても、応力が厚さ方向に一様に分布するか、あるいは直線的に変化するものならば「板」と見なして構わないはずです。このあたりも後ほどふれます。 片持ち梁を例にとり、それぞれの方法でどのようにモデル化されるかを下図に示しました。 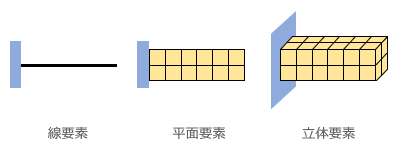 要素と節点 私たちはよく「変位法」と言いますが、これは「変位を未知数として応力を求める手法」を指すものです。そういう意味では、対象が線であれ面であれ、「有限要素法 = 変位法」なのですが、ここでは建築構造分野の慣例にしたがい、線材を対象とした有限要素法を「変位法」と呼ぶことにします。で、その変位法ですが、これはその名の通りの「節点の変位を求める方法」でした。そして、 ・節点の変位が分かれば部材のひずみ ( 変形 ) が分かる ・部材のひずみが分かれば部材の応力が分かる という手順で応力 ( 正確には「内力」ですが ) に到達します。 そしてここにいう節点とは、部材 (= 線要素 ) の境界点、すなわちその「両端」です。 この考え方は対象が「面」になっても変わりませんが、この場合の節点は要素の「頂点」です。 さきほど例示したような四角形の平面要素であれば、ここには 4 個の節点があります。下図のように、まず、これらの節点が外力の作用によってどのように位置が変わる ( 変位する ) かを求める。そしてその後は、「節点の変位」が分かれば「要素のひずみ」が分かり、「要素のひずみ」が分かれば「要素の応力」が分かる、という流れです。 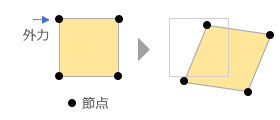 ところで、有限要素法が「節点の変位から要素のひずみと応力を求める」のであれば、節点の数が多いほど計算の精度が上がるはずです。単純に節点数を増やすなら細かく分割して要素数を増やせばいいのですが、これをもう少し効率的に行うために 2 次節点 あるいは 中間節点 と呼ばれるものがよく使われます。 これは要素の頂点をなす節点 ( 1 次節点 あるいは 主節点 ) の間にもう一つの節点を設けるもので、下図に示す通り、これを使えば四角形要素は計 8 節点で構成されることになる 。またこれにより、より柔軟な要素形状が作れることも下図から分かると思います。 1 次節点のみで構成された要素を 1 次要素、2 次節点があるものを 2 次要素 と呼びます。 ━━なお、ここまでは平面要素の形状をもっぱら四角形で描いてきましたが、「そうでなければならない」というものではありません。最もシンプルなのは三角形要素です。一方、立体要素としては六面体や四面体がありますが、汎用性の高い四面体がよく使われます。 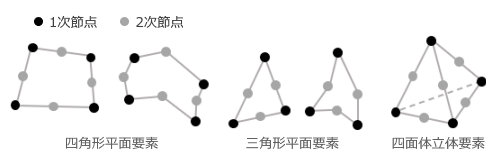 となると、次の問題は「どのように分割するか」ですが、多くの場合、この作業はプログラムによって行われます ( 自動メッシュ分割 ) 。 したがってその話題は飛ばし、有限要素法の理論の方に進むことにします。 次へ その1 その2 その3 その4 その5 その6 |