|
2018 年 1 月に積雪荷重の割り増しに関する告示が出されました。 平成 26 年の大雪によって多雪区域以外の建物の屋根が崩落する事故がありましたが、その主たる原因は、積雪後の降雨による雪の荷重の増大にあったと推定されています。今回の改正はそれを受けてのもので、実際に施行されるのは 2019 年 1 月になるようです。 まだ少し先の話ですが、その後であれこれ言われるのが面倒であれば、今から先取りして積雪荷重 ( 具体的には雪の単位体積重量 ) を割り増しておこう、という考え方もあるでしょう。 というわけで、今回はその内容についておさらいしておくことにしますが、ここでは、その理論的な背景ではなく、「どうやって計算したらいいのか」というもっぱら実用的な内容を取り扱います。 また、当社のウェブサイトで「積雪荷重の割増係数」という簡単なフリーソフトを公開していますが、これはそのマニュアルの役割も果たしています。 さて、この告示で対象になっているのは以下のような構造物です。
一方、フラットな陸屋根の場合はどうなのかというと、下図右にあるような「スパン長」とし、「水勾配」を屋根の勾配とする、とされています ( ただし実用計算上は勾配を 0 とすることが多いでしょう ) 。 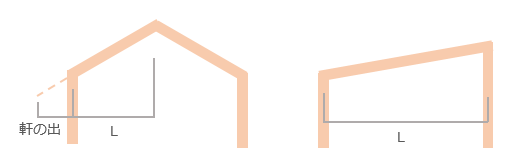 積雪荷重の割増係数 α の算出式は以下の通りで、これを「通常の積雪荷重」に掛けるわけです。この値は必ず 1 以上になるわけではありませんが、1 を下回る場合は 1 とします。 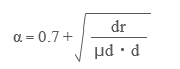 μd は屋根形状係数 ( 屋根勾配に応じた積雪荷重の低減係数 ) で、これを考慮する ( = 雪止めがない ) 場合は従来通りの式で求めます。つまりこの場合、いったん積雪荷重を割り増した後、それに低減係数を掛ける、という少々複雑なことになるわけです。d は垂直積雪量 ( 単位 メートル ) 。 よく分からないのは dr という値で、単位は長さ ( メートル ) 。説明がないので推測するしかありませんが、おそらく「降雨による荷重の増大が生ずる積雪深度」あたりではないでしょうか? だから添字の r は rain の略だろうと勘繰っているわけですが、それはともかく、告示では以下のように値が定められています。
ここでまず気になるのが、屋根勾配の単位が「角度」になっていること。 一般の設計者にとって、勾配を角度で表わす習慣はほとんどありません。よく「三寸勾配」 というようなな言い方をしますが、これは角度 θ の時の tanθ が 3/10 ( = 0.3 ) になるという意味です。ちなみに 15 度の tanθ は 0.268、2 度の値は 0.035 です。したがって、三寸勾配の屋根はぎりぎりで本規定の「圏外」になります。 先ほどの表に戻りますが、ご覧の通り、ここには「とびとび」の値しかありません。そして告示本文によれば、この「とびとび」の間は「直線補間しなさい」となっている。 ここには「水平投影長さ」「屋根勾配」という二つの変数がありますから、結局ここでは「二重の直線補間」が必要になりそうです。なんだか頭が混乱してきますが、とりあえず、屋根勾配と dr の関係をプロットしたものを下に掲げてみましょう。 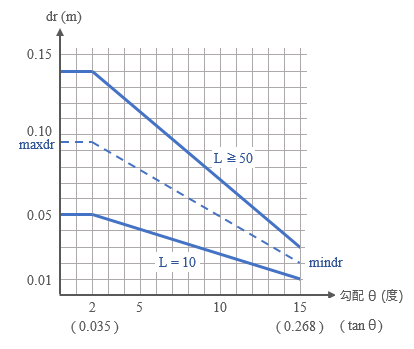 上側の青い線は L が 50m 以上のもの、下側の線が 10m のもので、それぞれ勾配が 2 度と 15 度の間を直線で結んで「補間」しています。 任意の水平投影長さ L ( 10 < L < 50 ) に対応する折れ線 ( 上図の破線 ) はこの 2 つの線の中間にあるはずですが、この時の dr の最大値 maxdr と最小値 mindr は下式で得られます。 maxdr = 0.05 + ( L – 10 ) ( 0.14 – 0.05 ) / ( 50 – 10 ) = ( 27.5 + 2.25 L ) / 1000 mindr = 0.01 + ( L – 10 ) ( 0.03 – 0.01) / ( 50 – 10 ) = ( 5 + 0.5 L ) / 1000 これらの値を使うと、任意の勾配 θ ( 2 < θ < 15 ) の時の直線補間による dt は下式で表わせる。 dr = mindr + ( 15 – θ ) ( maxdr – mindr ) / ( 15 -2 ) この dr を冒頭に掲げた式に代入すると割増係数 α が得られることになりますが、注意したいのは、ここで新しい変数として「垂直積雪量」が加わることです。 割増係数の一般的な傾向としては以下のようなことが言えます。 1. 積雪量が小さいほど割増しは大きい 2. スパンが長いほど割増しは大きい 3. 勾配が緩いほど割増しは大きい 1 については、全体の積雪荷重が大きいほど降雨後の荷重増大の影響が相対的に小さくなる ( つまり「降雨後の増大量 / 全体の積雪」の分母が大きい ) という理屈で説明できます。 2 はスパン長が大きくなるほど dr が大きくなることがもたらす効果です。さきほど、この値を「降雨による荷重の増大が生ずる積雪深度」と説明しましたが、それだけではなく、ここにはスパン長に応じた安全率が乗じられているのでしょう。 3 は現行基準にある屋根形状係数と同様の考え方です。 既述のとおり、この割増係数には「スパン長」「屋根勾配」「積雪量」という三つの変数が関わっています。だから「大体これくらい」という「当たり」をつけるのが難しいのですが、最後に、積雪量に応じて割増係数 α がどのようになるかを試算した結果を下に示しておきます ( 屋根形状係数は考慮していません ) 。
ツイート | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||