|
――というようなことを、先ごろ公開した「スマホで構造計算」を操作しているうちに思い出しました。 その上で考えたのは、「やっぱり手計算というものは必要なんじゃないか」ということ。なにも「もう一度手計算に戻ろう」などと言い出すつもりはありませんが、それにしても自分の中には、「手計算ができない構造屋さんは信用できない」という偏見がいまだにあるような気がします。 というわけで、いきなり「スラブの応力計算」の話です。 手計算の場合、話を単純にするために「版」を「単位長さの ( スラブ厚分のせいを持つ ) 梁」に置き換えてしまいます。 下図にあるのは等分布荷重 w が作用するスパン Lx のスラブですが、ここでは二辺が固定され、直交する辺が自由になっているものとします。ここから単位幅のスラブを切り出すと、これは「等分布荷重 w が作用するスパン Lx の梁」です。したがって、構造力学の公式さえ知っていれば、ここにあるような曲げモーメントの値が直ちに計算できるでしょう。 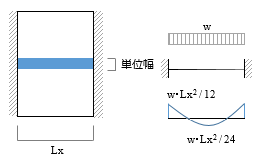 ここではスラブの上下辺を無拘束の「自由辺」と考えましたが、これを「固定辺」とすれば、ごく普通の「四辺固定」のスラブです。ではこの時、上と同様に単位幅の梁を切り出したならば、そこに作用している等分布荷重は w になるでしょうか ? ならないような気がします。なぜなら、この梁は直交方向にも引っ張られているからで、この値は必ず w よりも小さくなるはず。そして実は、これが冒頭に紹介した wx という値なのです。 そこで長い方の辺の長さを Ly とし、下図にあるように、この方向にも単位幅の梁を切り出してみます。 この時、スパン Lx の梁の荷重を wx, スパン Ly の梁の荷重を wy とすれば、w が wx と wy に「振り分けられる」と考えることができるので、この両者の和は w に等しくなる。 となると、次の問題は「 wx と wy をどのようにして求めるか」です。 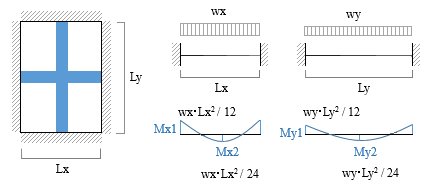 上の図にある青色の十字は、いわゆる格子梁 ( 交差梁 ) を形成しています。そして、格子梁の応力計算の定石は「格子点の変位を等値する」です。 等分布荷重 w を受けるスパン L の両端固定梁の中央部の変位は、定数 C と弾性剛性 EI により表わすことができます。そこで両方の梁の中央部の変位を等値すると下式が得られますが、これを整理すると右のように変形できます。 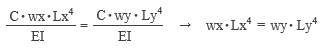 上の右の式に wy = w – wx の関係を代入した上で wx に関して解くと以下が得られます。これが RC 規準 10 条「スラブの解析」に載っている式です。 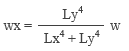 ところで、スラブの形状をあらわす際に、私たちはよく辺長比 λ ( = Ly / Lx ) という値を使います。そこで、上式の右辺の分子と分母を Ly4 で割って整理すると以下の式が得られます。 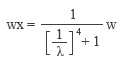 ここで、λ の値が大きくなる ( 全体形状が「細長く」なる ) と、上式の分母の 1 / λ の値は 0 に近づき、それに伴って wx の値は w に限りなく近づくことが分かります。 ちなみに、λ を 2 とすると wx = 0.94 w ――つまり、辺長比が 2 を超えるあたりから、四辺固定版が実質的な「一方向版」になってしまうことをこの式は教えています。 最終的に、短辺方向の端部の負曲げモーメント Mx1 と中央部の正曲げモーメント Mx2 は以下のように定義されることになりました ( ここにある Mx2 の係数 1/18 の理論値は 1/24 ですが、これは「周辺固定度の減少を考慮して安全側に割り増した」ものらしいです ) 。 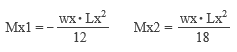 ここまで述べてきたのは、スラブの「中央部」に格子梁を仮想したものです。これはもちろん、短辺・長辺とも、直交する辺の拘束の影響が最も少ない中央部で最大応力が発生することが予想されるからです。 一方、スラブの隅部に近い領域の応力は、これよりも小さくなります。そのため規準では、隅部に近い領域では上記の値を 1/2 にしてよいと定めているのですが、しかし現在、スラブの隅部で鉄筋量を減らすという設計を行うことはほとんど皆無でしょう。 しかしながら、スラブはあくまでも「版」であって「梁」ではありません。「格子梁」というモデルは、計算の便宜のために頭の中でこしらえたものに過ぎない訳ですから、この値が「実際」とどの程度違うのか、ということは頭に入れておく必要があるでしょう。 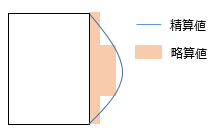 上の図は ( 規準書の解説等にも載っていますが ) 平面板の曲げモーメントの精算値と格子梁モデルによる略算値の比較を示したものです。 ここに見る通り、略算値から得られる応力は精算して得られる最大応力よりもつねに小さく ( 約 1 割程度 ) なります。しかし、「平面板の応力が耐力を局部的に超えていても、それが一定の範囲にまで広がらない限り大変形に至ることはない」という知見に基づいて略算式が是認されているようです。 これで短辺方向の話は終わりです。 次は長辺方向ですが、これも短辺方向と同様の理論に基づいて決めてしまえば簡単ではないか、という気がします。でもなぜか、そうはなってません。 先ほども述べた通り、この理論によれば、長辺方向の応力は辺長比が大きくなるにつれて小さくなり、辺長比が 2 を超えるあたりからはほとんど 0 になる。しかし実務設計上、それは好ましくないだろう、という考え方が一つあります。 それからもう一つ、実際に応力を精算してみると、長辺方向の応力は辺長比の影響をほとんど受けず、ほぼ一定値をとる、ということが分かりました。つまり、辺長比 1 ( 正方形 ) の時の応力を見ておけば、その後でどのように辺長比を変えてみても、( 短辺方向の応力が変わるだけで ) 長辺方向に関しては元の応力がそのまま保持されている、という事実です。 そこで辺長比が 1 の時の応力を求めてみますが、この時の wx は w / 2 になるので、先の式の wx にこれを代入すると、短辺方向の端部曲げモーメント Mx1 は下のように求められます。 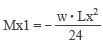 正方形なので、長辺方向の端部曲げモーメント My1 も上に等しい。同様の考え方を中央部にも適用すれば、結局、長辺方向の応力は以下で計算できることになります ( この時のスパン長が Ly ではなく Lx になっていることに注意 ) 。 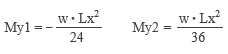 ( 文責 : 野家牧雄 ) |