|
知っておきたい振動解析 その 2
振動方程式
|
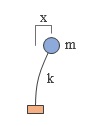
左にあるような、質量 m・バネ定数 k の一質点系に最初に何かの衝撃を与えると、後はそのまま放っておいてもしばらくの間揺れ続けます。これは 自由振動、つまり直接的に加わる外力がないのに揺れている状態で、地震が止んだにもかかわらず揺れつづける建物がこれに該当します。
この時の質点の変位量 x の遷移が「振動」と呼ばれる現象ですが、「その 1 」で述べた通り、この大きさは周期的に変化し、以下の式であらわされます。
x = A・cos ωt + B・sin ωt
|
ここにある t は時間、ω は質量 m とバネ定数 k から求められる角速度です。
A と B は系の初期条件によって定まりますが、途中を飛ばして結論だけをいうと、上の式は最終的に振幅 C の正弦波をあらわす下のような式に変換されます ( φ は初期条件によって定まる位相角 ) 。
x = C・sin ( ωt + φ )
次に、これを「力の釣合い」という観点から見てみましょう。
この質点に生じている加速度は変位 x を時間で二度微分したものなので、これを 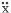 ( ツードット ) というふうに表記する習慣があるのですが、これを使うと、この質点に作用する力は m ( ツードット ) というふうに表記する習慣があるのですが、これを使うと、この質点に作用する力は m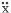 です。 です。
ただし、この力が「どちら向き」に作用するかが問題になります。
( 使い古された喩え話ですが ) 止まっている電車が急に動き出すと、乗客は進行方向とは逆向きに押されたように感じる。これが 慣性力 で、物体が「元の状態に留まりつづけよう」とする「惰性」をもつことに由来するものです。したがって変位方向を正とした場合、この力は負符号をつけて - m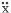 とするのが正しいことになります。 とするのが正しいことになります。
さらに、ここにはもう一つの「力」が存在します。
先の喩え話をつづけると、それは体が倒れようとする時に踏ん張って抗う力で、この力の向きは明らかに電車の進行方向を向いています。 質点系でいえば、この抵抗力はバネ定数 k であらわされ、その向きは質点の変位方向に等しく、フックの法則によれば kx です。
結局、これらの力の釣合いは
- m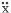 = kx = kx
とあらわされます。もう一度まとめておくと、
揺れている質点には「慣性力」が働いており、それに抵抗するのがバネの力である
これらの力の向きは逆で、釣り合っているのだから絶対値は等しい
ということです。
で、これを移項すると下の「力の釣合い式」になる。これが 振動方程式 で、この微分方程式を解いた答えがさきほどの「正弦波」なのです。
m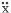 + kx = 0 + kx = 0
ところで先ほどの「答え」ですが、これは質点が振幅 C で「永遠に」揺れつづけることを意味します。
しかし、実際にはそうなりません。揺れているものを放っておけば、その振幅は徐々に小さくなり、やがて静止してしまう――これが 減衰 と呼ばれる機構です。
物理学的には「運動エネルギーが熱エネルギーに変換され、失われる」ということなのでしょうが、一般的な要因としては「空気抵抗」や「材料の分子間の摩擦」などがあげられます。
その昔、「五重塔はなぜ地震に強いのか」という議論が研究者の間で沸き起こった時、「接合部の独特の形状が減衰をもたらす」と説いた著名な論文がありますが、そのような、たとえば「部材の接合部の緩み」のようなものも減衰をもたらすと考えていいでしょう。
このように減衰という機構は複雑で捉え難いのですが、いずれにしても、これが揺れを抑制する方向に働くことは間違いありません。そこで工学的には、ここに「減衰力」とでも呼ぶべき「抵抗力」が作用していると考えることにしました。
振動理論では、この力は質点の「速度」に比例すると考えます。
速度は変位を時間で微分したものなので 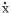 ( ワンドット ) と書きますが、これに 減衰係数 c を掛けた cx が減衰による抵抗力です。これにより、さきほどの振動方程式は下のように修正されます。 ( ワンドット ) と書きますが、これに 減衰係数 c を掛けた cx が減衰による抵抗力です。これにより、さきほどの振動方程式は下のように修正されます。
m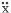 + c + c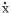 + kx = 0 + kx = 0
以下、この減衰係数というものの正体について見ていくことにします。
| 1 | 2 | 3 | 4 | 5 | 次へ
|