波の合成と分解

前回の「 Ai 分布の精算について」の中で「多質点系の複雑な応答を複数の一質点系の応答の重ね合わせによって表わす方法 ( モード合成法 ) 」を紹介しました。これは「一見複雑な現象を単純な事象の組み合わせに分解して理解する」ということになりますが、同じような考え方に

　時刻 t に関して周期的な値をとる関数 f (t) は複数の正弦波の重ね合わせによって表わせる

というのがあります。
これはフーリエ変換――ちなみにシャルル・フーリエは 18 世紀のフランスの数学者――と呼ばれるもので、式にすると下の通りです ( ここにある ω は合成された波形の角速度、「・・・」の部分は合成された波の数だけ式が続くことを表わす ) 。

　f (t) = a0 + a1・sinωt + a2・sin2ωt + a3・sin3ωt + ・・・+ b1・cosωt + b2・cos2ωt + b3・cos3ωt + ・・・

ただし、ここで私たちが知りたいのは波の合成と分解という「ものの考え方」だけなので、この式から「枝葉」を切り落としてしまいましょう。
まず第一項の a0 ですが、これは時刻 t に関係しない定数で、波形全体を上下に一定値だけ移動させる効果をもちますが、この値を 0 にします。さらに、波形の始点がつねに原点位置にあるものとすれば cos 波の項を無視できます ( これが sin 波と cos 波の重ね合わせになっているのは、波が原点位置から始まらない状態を表わすためなのです ) 。
すると、さきほどの式は下のように単純化されます。

　f (t) = a1・sin ωt + a2・sin 2ωt + a3・sin 3ωt + ・・・

これだけの準備をした上で、実際に波を合成してみましょう。



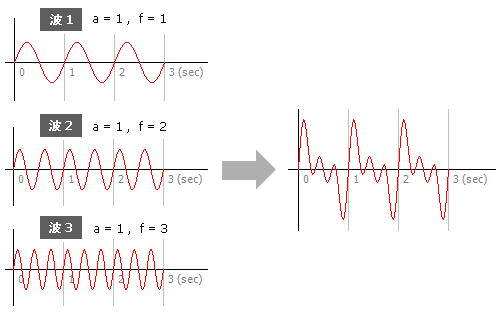
図の左側にあるのはいずれも振幅 a が 1 の正弦波で、振動数 f は上から1・2・3となっています。ここにあるのはその 3 秒分の波形記録ですが、では、これら三つを足し合わせた波形の振動数はいくらになるでしょうか ?
その答えは簡単に予想できます。
どの波形も 1 秒後には始点と同じ位置に戻って来る。そして以降は同じことを繰り返すのですから、合成した波形の周期は 1 秒で ( その逆数の ) 振動数は 1、さらに角速度は 2π ( = 2π ・1 ) です。
( なお、以下の話では「振動数」と「角速度」を時に応じて使い分けているので多少混乱するかもしれませんが、後者は前者の値に 2π を掛けただけのもので、「実質的には同じ」と考えてください。 )

合成した波形を図の右側に示しましたが、結局、これは以下の式で表せることになります。

　f (t) = 1・sin ωt + 1・sin 2ωt + 1・sin 3ωt

この例題は式をなぞっただけの、いわば「そのまんま」ですが、しかし少なくとも、ここから

合成後の波の振動数は個々の成分波の振動数のうちの最小値を上回ることはない
もしくは
合成後の波の周期は個々の成分波の周期の最大値を下回ることはない

ということは分かるはずです。
なぜならば、合成後の波が 1 サイクルを終えた時点では、すべての成分波が最低でも 1 サイクルは終えていなければならない。ある成分波が 1 サイクルを終える前に合成後の波が 1 サイクルに達することはありえないのです。
したがって、たとえば先ほどの図にある「波 1」と「波 3」を合成した波の振動数もやはり「波 1」の振動数と等しくなり、( この場合の「波 2」は「振幅 0」と見なせるので ) 以下の式で表わされます。

　f (t) = 1・sin ωt + 0・sin 2ωt + 1・sin 3ωt

ここで取り上げたのは、「個々の成分波の角速度 ( = 振動数 ) のうちの最小値が ω で、他の成分波の角速度がその整数倍で表わせる時、合成後の波の角速度は ω になる」という例題です。じつはこの「整数倍」というのがポイントになるのですが、しかし、いつもそんなにうまく行くはずがありません。
そこで次に、整数倍になっていない例を見てみることにしましょう。



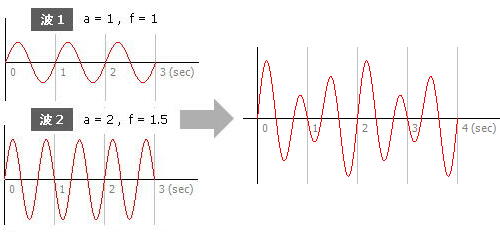
ここにある「波 1」はさきほどと同じものです。「波 2」の方は振幅 2 ・振動数 1.5 で、今回は振動数が整数倍になっていません。これらを合成した波の振動数がいくつになるかを考えてみます。
波形を見比べれば分かるように、この二つの波は 2 秒後、つまり「波 1」が 2 サイクルを終え、「波 2」が 3 サイクルを終えた時点で出会います。以降はここを始点とした繰り返しですから、合成後の波の周期は 2 秒、振動数は 0.5 になるはずです ( 右側に示した合成後の波形で確認できます ) 。
そこで、合成した波の角速度を ω ( = 2π ・0.5 ) とすると、今回は最初の ω の波はなく、 2ω ならびに 3ω の波だけなので、合成後の波形は以下の式で表わされます。

　f (t) = 0・sin ωt + 1・sin 2ωt + 2・sin 3ωt

さて、ここでもさきほど述べた「合成後の波の振動数 ( 角速度 ) は個々の成分波の振動数 ( 角速度 ) のうちの最小値を超えることはない」という原則が生きていることが確認できるでしょう。
ただし先ほどと違い、振動数は最小値 ( この場合は「波 1」の 1 ) の 1/2 になっている。結局、こういうことなんです。

• 合成後の波の角速度 ω は個々の成分波の角速度のうちの最小値を整数で割った値になる
• そしてこの ω を使うと、個々の成分波の角速度はその整数倍で表わされる

それにしても、なぜ「整数」なのか ? ――それは波の「周期性」によって説明できます。
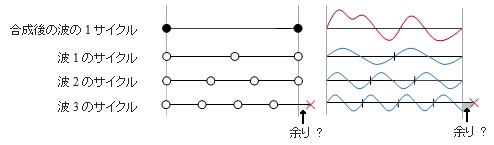
合成後の波の 1 サイクル ( 周期 ) は個々の成分波のサイクルをすっぽりと包含するようなものでなければならないはずです。
つまり、合成後の波が 1 サイクルを終えた時点では、すべての成分波もきっちりと「整数回」のサイクルを終えていなければならない。そこに変な「余り」があってはいけないのです。だから「整数倍」なのですが、念のため下に図解してみました。

以上が波の合成と分解に関する基本的な考え方です。
「合成」の方はともかく、「分解」ということになるといろいろ技術的に難しい問題がありそうな気がしますが、そのあたりは「合成できるのなら分解だってできるはず」ぐらいに考えておくことにしましょう。以下では、その分解した結果を図的に表わす スペクトル というツールを見ておくことにします。
これは「対象とする波の中にどのような成分の波がどのような強さで含まれているか」をグラフで表わしたものです。ここで取り上げた最初の例題のスペクトルが下図の左、二番目の例題のスペクトルが右になります。

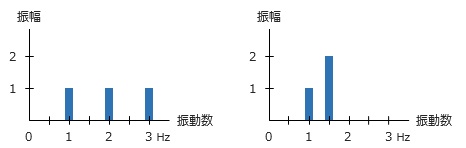
通常は横軸に「振動数」をとります ( その逆数の周期をとることもある ) 。
縦軸は「振幅」ですが、これはは必ずしも「変位」を指すわけではありません。対象とするものが速度波であれば「速度」、加速度波であれば「加速度」になりますが、ただし、変位振幅が分かれば他のものを簡単に求めることができます。
変位を時間で微分したものが速度で、さらにそれをもう一回微分したものが加速度ですが、ここで三角関数の微積分の公式を思い出してください。sin ω t を t に関して微分したものは ω・cos ω t になるのでした。ようするに、位相がずれるだけです。したがって、これをフーリエ変換の式に当てはめてみると、変位振幅を d (t) とした時の速度振幅と加速度振幅は下のような簡単な式で表わされることが分かります ( この式は後ほど再び登場します ) 。

　速度 v (t ) = ω・d (t) = 2π f ・d (t)　,　加速度 a (t ) = ω・v (t) = ( 2π f ) ・v (t) = ( 2π f )² ・d (t)

これは正確には パワースペクトル というものになりますが、これとよく似た フーリエスペクトル というのもあります。両者の違いは縦軸の値の取り方だけで、フーリエスペクトルではこれを「振幅に波の継続時間の 1/2 を掛けた値」とします ( したがって、たとえば加速度スペクトルであれば gal・sec のような単位になる ) 。
それから、最後にもう一つ。
ここではスペクトルを「棒グラフ」で描きましたが、実際にはギサギザの「折れ線グラフ」で表わされることが多いかもしれません。しかしここまでの話で分かるように、これは ω ・ 2ω ・ 3ω ・・・ という「とびとび」の角速度をもつ波について表わしたもので、その「間」は存在しません。
ですから、たとえば上図の右のグラフで、棒グラフの二つの頂点を結ぶと右上がりの折れ線が出来上がりますが、これは、その区間で振幅が右上がりに遷移することを表わしているわけではありません。折れ線グラフで描かれている場合、意味をもつのはその折れ線の「頂点」だけであることに注意してください。