曲げ応力度と剪断応力度
ここまで、耐震壁を例に「純剪断」という状態を取り上げてきましたが、これは「水平方向の力によって断面が水平方向にずれる」ものです。そういう意味では大変分かりやすい。
しかし、断面が「ずれる」方向に明確に力が作用していない場合でも剪断力が発生することがあります。それが「曲げモーメントの変化によって生じる剪断力」です。
長さ L の単純梁の両端に逆向きの曲げモーメント M を作用させると、梁の全長にわたって曲げの値は一定になり、剪断力は 0 になる。これに対し、一端のみに M を作用させた時の曲げモーメント図は、他端で 0 になるような直線になり、ここに M / L という大きさの剪断力が発生する――これまた「何をいまさら」でしょうが、下に図示しました。
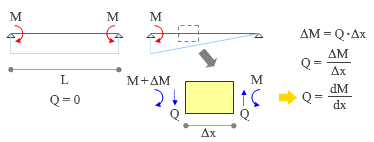
この図の右側にあるのが「曲げモーメントが変化すると剪断力が発生する」理屈の説明です。
長さ ⊿x の区間を取り出した時、左側の切断面の曲げが M + ⊿M で右側の切断面が M であるとすると、ここでは明らかに曲げモーメントの釣り合いが成り立ちません。
ここに Q・⊿x という曲げモーメントを介在させ、この値を ⊿M と等しいと置くことによって初めて釣り合いが保たれる。この Q が剪断力であり、さらに ⊿x → 0 という条件のもとで dM / dx = Q という関係が成立する。
これが「曲げモーメントの微分値が剪断力である」の説明ですが、しかしそれにしても、よく分からないのはこの時の「剪断変形」です。
剪断変形は断面に「ずれ」をもたらすはずなのですが、この時の「ずれ」は一体どこからやってくるのか?
この「ずれ」に関して以下のような説明がよく使われます。
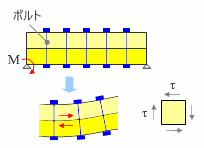
下図に示したのは、二枚の板を一定の間隔で通しボルトで締め付けて一体にした梁材です。
これにさきほどと同様の時計回りの曲げモーメントを加えると、この部材は「下が凸」の曲げ変形をしますが、この時、二枚の板は互いに「ずれよう」とする。そしてその「ずれ」に対してボルトが抵抗しようとするので、このボルトに「剪断力」が発生する、というわけです。 注 )
注 )
ただしこの時、もう一方の端部に同じ大きさの逆向きの曲げモーメントを作用させ、梁の曲げを一定に保っているならば「ずれ」は生じない。これは曲率が一定になっている状態で、ようするにすべてのボルトの延長線が一点 ( 円の中心 ) で交わることを意味します。
もちろん、実際の梁がこのように二枚の板をつづり合わせて作られているわけではありませんが、ボルトの代わりに強力な接着剤で貼り合わせてあると考えても同じですし、引いては一枚の板で一体に作られていると考えても同じことになります。
断面内を微視的に観察してみれば、そこには部材軸方向に「ずらそうとする力」が働いており、そしてそれに抵抗しようとする剪断応力度 τ ――この力は上図に示す通り、部材軸に沿った切断面に存在すると同時に、それとの釣り合いを保つため、部材軸と直交した切断面内にも同じ大きさで存在する――が発生するのです。
ところで、この梁が部材軸方向に引っ張られたり押し込まれたりする要因があるとすれば、それはここに生じている曲げ応力度、すなわち曲げモーメントに伴って生じる引張あるいは圧縮応力度以外にはありえません。それが「ずらそうとする力」を生んでいるのです。
さきほどは二枚の板を貼り合わせた状態を考えましたが、ここでは薄い板を何枚も貼り合せた状態を考えてみます。この時、一枚の板に生じている「ずらそうとする力」は、それよりも上 ( あるいは下 ) にある個々の板材に生じている力の累積値になることは容易に理解できるはずですが、このあたりの事情を下図にしたがって見ていくことにします。
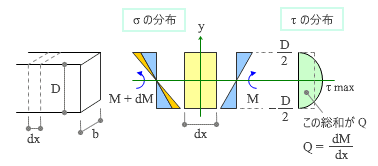
これは、曲げモーメントを受けている梁――梁幅 b・梁せい D の長方形断面――の微小区間 dx を切り出して応力度の分布を表したものです。
ここで、右側の断面に生じている曲げを M、左側の断面におけるそれを M + dM とすると、この不釣合い分の dM こそが「ずらそうとする力」を生むことになる。これによって生じる曲げ応力度 ( 引張あるいは圧縮 ) の分布を上の図ではオレンジ色に塗りつぶしておきました。
まず、断面の下端 ( y = - D / 2 ) における不釣合い力を考えてみます。
その大きさは、そこよりも上部にある不釣合い力の総和――オレンジの塗りつぶし部分の総面積に相当する――になりますが、その向きは中立軸 ( y = 0 ) を境にして反転し、さらに中立軸の上下で同じ大きさをとりますから、明らかに 0 になる。そしてこれは、断面の上端 ( y = D / 2 ) において「それよりも下部にある不釣合い力の総和」を考えた時も同様です。ここから、
左右断面の不釣合い力 ( ずらそうとする力 ) は断面の中心で最大値をとり、縁で 0 になる
という予測がつきます。この力の大きさがそのまま断面内に生じる剪断応力度 τ に相当するわけなので、その分布は上図の右に示したようなものになっているはずです。
それが具体的にどのように分布するか、という話に入る前に、ここで論点を整理しておきましょう。
この断面内における τ の「総和」なら私たちはすでに知っています。それは剪断力 Q であり、( すでに何度か出てきたように ) Q = dM / dx です。この値を単純に断面積 A で割った値 ( Q / A ) が 平均剪断応力度 です。
上図右にある τ の分布図中に平均剪断応力度の値を破線で示しましたが、あらためて言うまでもなく、断面内に実際に生じている最大剪断応力度 τmax はこれよりも必ず大きくなります。
したがって、τ がどのような分布をとるのかを知ると同時に、「最大剪断応力度は平均剪断応力度に比べてどれれくらい大きくなるのか」について知っておくことも無益ではないでしょう。
下図にあるのは、さきほど切り出した梁断面を、さらに図心軸から y1 だけ離れた位置で水平に切り出したものです。この断面の下辺に生じている剪断応力度を τ 、これによる力を T1 とすれば、その値は 式-1 にあるように表せることになる。これが図でオレンジ色に塗りつぶした部分、つまり左右辺に生じている曲げ応力度の差によって生じる T2 ( ずらそうとする力 ) と釣り合うはずです。
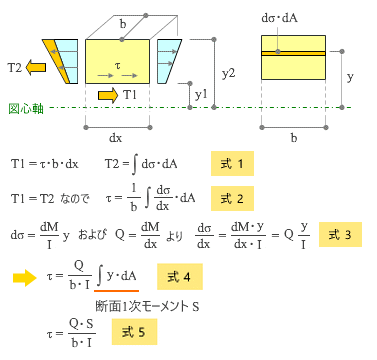
図の下側にあるように、図心軸から y の距離にある部分の断面積を dA、この部分の ( 左右断面の曲げ応力度の差によって生じる ) 応力度を dσ とすれば、T2 は dσ・dA を y = y1 から y = y2 まで積分した値です ( 式-1 ) 。
そこで T1 と T2 を等置し、さらに変形すると 式-2 になります。
ここにある dσ / dx という値は、σ = ( M / I ) y および Q = dM / dx というお馴染みの関係を使うと 式-3 のように書き直せる ( I は全断面の断面2次モーメント ) 。この関係を 式-2 に代入して得られるのが 式-4 です。
ところで、この右辺に見えている積分値は、この断片の図心軸回りの断面1次モーメントにほかなりません。そこでこれに S という記号を割り当てて書き直したのが 式-5 です。
ここで y1 の値を - D / 2 から D / 2 の範囲 ( D は梁せい ) で変えながら S の値を求めていけば断面内の τ の分布が得られることになります。 注 )
注 )
ちなみに、ここで y1 を - D / 2 あるいは D / 2 とすると、「図心軸回りの断面1次モーメントは 0 になる」という原則にしたがって S が 0 になり、したがって τ も 0 になる。先に述べた通り、「断面の縁では剪断応力度が 0 になる」のです。
断面積 A の部材に剪断力 Q が作用する時、その平均剪断応力度は Q / A ですが、断面の図心軸で発生する最大剪断応力度 τmax はこれよりも必ず大きな値をとります。そして 式-5 から明らかなように、それがどれくらい大きくなるかはもっぱら断面の形状に依存することになる。そこで、最大剪断応力度を平均剪断応力度で割った 形状係数 と呼んでいます。
長方形断面を例にとれば、式-5 に
I = b・D3 / 12
S = b・( D / 2 )・( D / 4 ) = b・D2 / 8
を代入することにより、
τmax = 1.5・( Q / ( b・D ) ) = 1.5・( Q / A )
の関係が得られる。長方形断面の形状係数は 1.5 になるのです。
次項では、ここに紹介したような考え方が実際の断面設計にどのように生かされているのかを見ていくことにしましょう。
前へ | 1 | 2 | 3 | 4 | 次へ
|